|
2009/9/12�@�V�����[�f�B���K�[�̈⌾
|
|
�����Ȋw�̂X�����@���W�^�V�����[�f�B���K�[��ǂ�ł��܂����Ƃ���A�ȉ��̂悤�ȕ��͂�����܂����B
�`�`�`�V�����[�f�B���K�[�����L�ɏ������A�⌾�Ƃ���������͉̂��L�̂Ƃ���ł���B
�Ȃ��Ȃ�A������̂͂���ꂪ���̂��̂������邪�̂ɂ���̂ł͂Ȃ��B
�����āA���̂��̂��Ȃ��̂͂���ꂪ���̂��̂������Ȃ����̂ł͂Ȃ��B
���̂��̂����݂��邪�䂦�ɂ����͂���B�����������I�ɂł���B
����䂦�A�����鑶�݂́A���ׂėB��Ȃ鑶�݂ł���B
�����Ă���l������ł��A�B��Ȃ鑶�݂����葱����Ƃ������Ƃ́A
���̐l�����݂���߂��̂ł͂Ȃ��Ƃ������Ƃ��N�ɍ����Ă���̂��B
���̕�ɊȒP�ȖؕЁi���Ƃ��Δ��̂ӂ��j�Ƀy���L�ł���������ĉ������B
����ǂ��A�ؕЂ����܂�ɂ����������Ă�����̂ŁA�������胂���^����
�h���Ă��������B���Ƃ͎v���c�����Ƃ͂���܂���B�`�`�`
����́A�V�����[�f�B���K�[�̎��̂Q�O�N�قǑO�ɏ����ꂽ���ł����A���̎����������ꂽ�͖̂v��S�O�N���o������̂��ƂŁA�������ɂ���Ė]�݂�������ꂽ�����ł��B
|
|
|
|
|
2010/5/5�@�a�ғN�Y�ɂ��u�@�v�̍l����
|
|
���Ď��m�̂悤�ɁA�����̘a�ғN�Y�́A���n�����̍��{�I���ꂪ���́u�@�̔F���v�ɂ��邱�Ƃ�����������Ă����B����̎咘�̈�ł���w���n�����̎��H�N�w�x���A���́u�@�̔F���v�ɂ��Č����������A���̐��i�𖾂炩�ɂ��悤�Ƃ�����̂ł��������Ƃ͂����܂ł��Ȃ��B���������Ď��ɂ��u�@�v�̖��ɂ���c�_�́A���R�̂��ƂȂ��瑽��ɂ킽���Ă���B���ꂼ��ɋ����[���e�[�}������Ă���̂ł��邪�A�����������ł́A����̂�����̘_�_�ɂ��ڂ��čl���Ă݂邱�Ƃɂ��悤�B
���̘_�_�Ƃ������̂��A�u�@�v�̖{���̈Ӗ����u�����v�Ƃ��ĂƂ炦�悤�Ƃ��錩���ɂ�����̂ł���B���ɂ��A�܂��A�������E�ɂ����ĕω����A�����ĉ߂��䂭���̂́A�����܂ł��Ȃ����ԓI���݂ł���B�����Ă��̎��ԓI�ȑ��݂��A�����ł́u�L�ҁv�Ƃ������B�Ƃ��낪����ɂ������āA�������̌������E�ɂ����ĕω��������A�߂��䂫�����Ȃ����̂��A�����ԓI�ɑÓ�������̂ł���B�����Ă��̒����ԓI�ɑÓ�������̂��A���n�����ɂ����Ắu����svabhava�v�������̂Ƃ���Ă���B�����Ƃ����̂́A�Ɨ������Ƃ��������炢�̈Ӗ��ł���B�ς�炴��{���Ƃ����Ă��������낤�B
���āA���ԓI�ɑ��݂�����͕̂ψՂ��ω����邩�疳��ł���B����Ƃ́A�P�퐫�������Ƃ������Ƃ��B�Ƃ��낪���̖���Ȃ���̂́A����Ƃ����u�����v�u�̂�v�ɂ����ėL��A���ω�����̂ł���A�Ƙa�҂͂����B�����Ă��̏ꍇ�́u�����v�u�̂�v�����Ȃ킿�u�@�v�Ȃ̂��Ƃ����B��������A����Ɂu����v�Ƃ����T�O������A�����Ɂu����Ȃ���́v�Ƃ����ω��E���ł��鎖��������B�ω��E���ł���X�́u����Ȃ���́v�́A�u����v�Ƃ����ϔO�i�������j�Ɏx�����đ��݂��Ă���킯�ł���B���ꂪ�a�҂́A����Ȃ���͖̂���Ƃ��������ɂ����Ăł���A�Ƃ����Ӗ��ł���B
�����ŁA����Ȃ���͕̂ψՂ���L�ҁi���݁j�ɂ����Ȃ����A���퐫���̂��̂́A����Ȃ�L�҂��x����Ƃ���̒����ԓI�ȁu�����v�i���@�j�ƍl�����Ă���Ƃ���ɒ��ڂ��悤�B�u���퐫�v�Ɓu����Ȃ���́v����ʂ��Ă���̂ł���B���Ȃ킿�a�҂́A��@�v�Ɓu�@�ɂ���đ��݂�����́v����ʂ����B�u�@�̗̈�v�Ɓu���݂̗̈�v�̂������ɖ��m�Ȉ�����������̂ł���B���̌��ې��E�ɂ����ẮA�߂��䂭���̂��ꎩ�̂��u�@�v�Ȃ̂ł͂Ȃ��B�߂��䂭���̂����̂��̂Ƃ��Ă��炵�߂���u�����v�Ƃ��Ă̂��̂��u�@�v�Ȃ̂ł���B�@�i�@�̗̈�j������Ȃ̂ł͂Ȃ��A�@�Ƃ����u�����v�ɂ����ė��]���Ă䂭���́i���݂̗̈�j������ł���Ƃ������ƂɂȂ�B
����Ԃ��Ă����A�a�ғN�Y�́A�@�̉��߂ɂ��Ė���Ȃ���̂͂����܂Łu���́v�ł����āA�u�@�v�ł͂Ȃ��Ƃ������Ƃ��������Ă���B���đ��ɑ�ȓ_�́A�u���݁v�Ɓu�@�v��O�q�̂悤�ɗ̈�I�ɕ������̂ł��邩��A�u�@�v�����Ȃ킿�u���́v�ł���Ƃ����l������ے肵�Ă��邱�ƂɂȂ�B�������Ă���̍l�������炷��A�u�@�v�͎����������A�����ԓI�ɑÓ�������̂ł����āA���ԓI���ݎ҂ł͂Ȃ��B�i���~�̐��_�j�@�����̃C���h�@�R�ܓN�Y���@�p��\�t�B�A���Ɂ@P87�`P89��蔲���j
����ǂa�ғN�Y�̌��ې��E�Ɋւ���Ƃ炦�����A�f�B�A�O���c�}�i�}�\�j�ŏ��������o�ɋ߂��Ǝv���܂����B
|
|
|
|
|
|
�@�،��@���c�q���̒����w�،��o�{���L�x�̂Ȃ��ł́A�u���͑̂Ȃ�A�N�Ƃ͐S�n�Ɍ��݂���̂݁v�ƒ�`�����B�@�����A�O���X�̐S�n�Ɍ��݂��Ă��邱�Ƃ������B�킽�������̐S�̂Ȃ��ɂ́A�قƂ��������卿���Ă���Ƃ������ƂɂȂ�B�����Ԃ������ďC�s���A�������ɔϔY���Ȃ����āA���ɐ��炩�ȂقƂ��̐S�ɂȂ�A�Ƃ����̂ł͂Ȃ��B�{���킽�������͐������Ă���̂��A�Ɛ����̂����N�ɂق��Ȃ�Ȃ��B
�@�킽�������̌����̐S�͔ϔY�ɂ������A������咣���A��Y�ɂ������ł���B�S���I�ɂ͂�邹�Ȃ��ǓƂɂ����Ȃ܂�Ă���B���̂悤�Ȃ����̐S���̂��̂��A�قƂ��̂��̂��̌����Ȃ̂��A�Ƃ����̂����N�̎v�z�ł���B�킽�������̈��Ƃ�ϔY�△���Ȃǂ̂��ׂĂ��A�u���N�v�ɂ��炴��͂Ȃ��̂ł���B�ϔY�△���∫�́A���̎��̂������̂ł͂Ȃ��A�قƂ��̐��E����݂�A�����͔݂ƂȂ�B�����ɔY�ނ����̐S�̂Ȃ��ɂ��A�قƂ��̌������ѓO���Ă���B�قƂ��̎��߂ɕ�܂�Ă���B����A�~�]���̂��̂��A�قƂ��̈��ɂق��Ȃ�Ȃ��B�O���̂���Ƃ���A�����ɂ͂��ł��قƂ�������B��y�ł͂Ȃ��āA�n�������قƂ��̂��݂��łȂ���Ȃ�Ȃ��B�Èł��قƂ��̌������ĂсA��Y���قƂ��̎��߂�G������̂ł���B�قƂ��̏o���͂܂������n���ɂ����Ăł���B���炪���ɂ����ɐ����A�������Ă������痣��邱�Ƃ��ł��Ȃ������̐��E�����A�܂��ɂقƂ��̂��݂��ɂق��Ȃ�Ȃ��B
�@�����Ƃ��A�قƂ��̂��̂��Ƃ������̂́A�O���Ɛ藣����đ��݂���̂ł͂Ȃ��A�O���Ƃ�����邱�Ƃɂ���āA���j���`�������H��W�J���Ă䂭�B�قƂ��̂��̂��͐��N�Ƃ��Č����ɂ͂��炫�A�͂��炭���̂�ʂ��āA�����ɐ����Ȃ���Ȃ�Ȃ��B�قƂ��̂��̂��Ƃ͏O���Ƃ̏o��ɂ����āA�O���Ƃ̂�����肠���ɂ����āA�O���Ƃ̔}��ɂ����āA�قƂ��͂͂��߂ĂقƂ��̂��̂������킵�Ă䂭�B
�@�����Ƃ͋�Y�̌����ł��邪�A���̐l���̋ꂵ���킢�E�����������A�قƂ��̂��̂����̂��̂Ȃ̂ł���ƌ����Ă���B���̐l�����ꂵ������Ƃ����Ă������瓦������A�قƂ��̂��̂����������ƂɂȂ�A�܂��t�ɂ��̏X���Ȑl���ɂȂ��̗��z�������������Ă䂭���Ƃ��A�قƂ��̂��̂��������䂦��ł��邱�Ƃ�����Ă���B�����̋����͂ǂ��܂ł����̌������̓����ł����Ă͂Ȃ�Ȃ��B���̓D�܂݂�Ȑl���̐^�����ɐ����邽�߂̗͂�^���A�m�M��^����̂��A�����̋����Ȃ̂ł���B�����łȂ���Ε����Ȃǂ͉ߋ��̈╨�ɂ����Ȃ��Ȃ낤�B
�@�V����،������������̐��Ƃ�������̂ł���A�Ƃ��Ɍ����̂Ȃ��ɐ^�������������Ƃ��������̐�m��_�ł���A���҂Ƃ����̂Ȃ��ɕ��Ղ̓��݂�F�߁A������O���ɐ�̉��l�������������`�ł͂��邪�A�V��ł͖�����}�v���قƂ��̂��̂��Ƃ��Ă̗쐫����L���Ă���Ɛ����A�،��ł͖}�v�͖{���I���ꂩ�炢���A���Ƃ��ƂقƂ��̂��̂�����o�Ă������̂ł���Ɛ����B�V��́u��v�̈ꎚ�A�،��́u�N�v�̈ꎚ�ŕ\�킳���B���͕��ՓI�ȂقƂ��̂��̂���{���Ƃ݂�̂��V��A��������͕̂��ՓI�ȂقƂ��̂��̂��̕\�������ł���Ƃ݂�͉̂،��ł���B�V��͖}�v�̗��ꂩ��قƂ��̂��̂����݁A�،��̓u�b�_�̗��ꂩ��}�v���Ȃ��߂�̂ł���B
�u�����̐��E��<�،�>�@���c�ΗY�E��R�t�����@�p��\�t�B�A���ɁvP170�`P177���甲���B
|
|
|
|
|
2010/6/6�@�Ԉ�������Ƃ͋N���邱�Ƃ��ł��Ȃ��B
|
|
�����グ���{�[������������`���̂́A���̋O�����ł��N����₷������ł��A�Ƃ������b�����������܂����B�o�H�ϕ��̍l�����ł́A�����グ���{�[���́A������O����ʂ�\��������܂����A�ŏ���p�̌����ɏ]���āA�ŏI�I�ɂ͕������̋O�����g�����̒����猻�ۉ����Ă���킯�ł��B
����ŁA�������͓��킢�낢��ȑ̌������܂��B�d�������܂��������肤�܂������Ȃ�������A�l�ԊW�����܂��������肤�܂������Ȃ������肵�܂��B�d�������܂������ق߂��A�d�������s������Ȃ���ċ��������������肵�܂��B�l�ԊW�����܂������Ȃ��Ȃ�Α��݂������荦�݂������肷����̂ł��B
�d�������܂������̂����̐��Ɍ��ꂽ���ۂł���A�d�������s����̂����̐��Ɍ����������ۂł��B�܂��A�l�ԊW�����܂������̂����ۂł���A���܂������Ȃ��̂���͂茰���������ۂł��B
�`���̃{�[���̗�̂悤�ɕ����̒��Ō��ۂƂ��Č��邱�Ƃ��ł��邱�Ƃ́A�ł��N����₷�����ƁA�܂�N����ׂ����ċN�����Ă��邱�Ƃł���Ƃ������Ƃ��l���܂��ƁA�l�ԎЉ�̒��ŋN�����Ă��錻�ۂɂ��Ă����̗�ɘR��Ȃ��̂ł͂Ȃ��ł��傤���B
�d���Ɏ��s�����Ƃ������ۂ��A���������������ۉ������Ƃ������Ƃ́A������̒��ł����Ȃ邱�Ƃ��ł��N����₷�������킯�ŁA�N����ׂ����ċN�������킯�ł��B
�l�ԊW�����܂������Ȃ��Ȃ��Ă��܂��������A�����Ȃ����Ƃ������Ƃ́A������W�̒��łȂ�ׂ����ĂȂ����킯�ł��B
��������`�����{�[���ɑ��āA��������`�����Ƃ͑P�����ƂȂ̂��������ƂȂ̂����c�_���Ă݂Ă����̈Ӗ����Ȃ��̂Ɠ����悤�ɁA�d���Ɏ��s�������Ƃ�l�ԊW�����܂������Ȃ��������Ƃɑ��āA�P�������Ɣ��f���邱�Ƃɂ��Ӗ����Ȃ��Ǝv���܂��B�N����ׂ����ċN�������̂�����A���������邵���Ȃ��̂ł��B�N���������Ƃ��B��u�������v���ƂȂ̂ł��B
�d����l�ԊW�̏ꍇ�ɂ́A�N���������ۂɑ��āA����͑P�������Ƃ��A����͈��������ȂǂƂ�������イ���f�����܂����A�{�[���Ɠ����悤�ɍl����A�N���������Ƃ��B��u�������v���ƂȂ̂ŁA�P�������ȂǂƂ����]���͗v��Ȃ��킯�ł��B
�������ۂƐl�ԎЉ�̒��̌��ۂ����̂悤�Ɍ��ѕt���Ă��܂��̂͒Z���I��������܂��A���Z�H�w�̒��ŏo�Ă���������ƕ����̒��ŏo�Ă�����������܂����������`�ł��邱�Ƃ����ɂƂ�A���Ȃ����I�O��Ȑ��_�ł͂Ȃ��̂ł͂Ȃ����Ǝv���Ă��܂��B
������Z�h�����i�̉��i�̌`����\���������́A�V�����f�B���K�[�������Ƃ܂����������`�����Ă��܂����A���i�̌`���ɂ͐l�Ԃ̊���傢�Ɋ֗^���Ă���̂������ł��B�ߋ��̊����̐��ڂ��L�^���������̃`���[�g�ɂ́A�l�Ԃ̗~�⋰�|����������Ɖf�����܂�Ă��܂��B
�u����͑���ɕ����v�Ƃ������t������܂��B
�����������������Ă��܂������ɒQ���Ă݂��Ƃ���łǂ��ɂ��Ȃ�܂���B
�N���������ƁA�N�����Ă��邱�Ƃ��B�ꎖ���ł���̂ŁA������ÂɌ��߂�A�Ƃ������t�ł��B�N���������Ƃ��B��u�������v�̂ŁA����ɉ��炩�̗��R�����Ď������Ԃ߂���A���������Ƃ����������ƌ�����Ă݂Ă��d���������̂ł��B
�����������ł���悤�ɁA�d���̌��ʂ�l�ԊW�ɂ��Ă��A�������Ƃ�������̂ł͂Ȃ��ł��傤���B
�����āA�l�ԎЉ�Ɍ���錻�ۂ��A�ЂƂЂƂ��ׂ������Ă䂯�A�����͑S�ĕ������ۂ̐ςݏd�˂ł���킯�ł��B
���̕������ۂ́A�o�H�ϕ��ƍŏ���p�̌����ɏ]���Ă��āA�����̉\���̒�����ł��N����₷�����Ƃ������Ă���̂��Ƃ������Ƃ��A���㕨���w�͖��m�Ɍ���Ă��܂��B
�ЂƂ̌��ۂ��������邻�̔w�i�ɂ́A�����̎̂Ă��Ă��܂����\�������݂���Ƃ����������l����A�N���������Ƃ��B��u�������v�̂��Ƃ������Ƃ������ł���̂ł͂Ȃ��ł��傤���B
���ۂ��������Ă��Ȃ��}�v�́A���̌��ۂɗD������A�Љ�ʔO��펯�A�@���ɏ]���ċN���������ۂɑ��đP���Ƃ������]���������܂����A�N���������ۂ̔w�i�ɂ́A�����̌������邱�Ƃ��ł��Ȃ������\�������݂��邱�Ƃ��v���A�����c���ĕ\�Ɍ���ꂽ���ۂ́A���Ƃ����ꂪ�Љ�ʔO��펯�̔��e�ł͈������Ƃł������Ƃ��Ă��A�Ȃɂ��ƂĂ��M�d�Ȃ��̂Ɏv���Ă��͂��Ȃ��ł��傤���B
�u�N���������Ƃ��B�ꐳ�����B�v�A������A�u�Ԉ�������Ƃ͋N���邱�Ƃ��ł��Ȃ��B�v�ƂȂ�܂��B
|
|
|
|
|
2010/7/19�@���̃��t�����iSoul's Refrain�j
|
|
|
|
|
|
|
|
�Љ�̃��[���Ƃ������̂́A���̎Љ�ɑ����Ă��镽�ϓI�Ȑl�X�̐U�镑���ɑ����č���Ă��܂��B
�Љ�̏펯�Ƃ������̂��A���̎Љ�ɑ����Ă��镽�ϓI�Ȑl�X�̍l���Ɋ�Â��ď����������̂ł��B
�Љ�ɂ́A��������̐l���������݂��Ă���A�l�X�Ȑl�����������Ă���̂ŁA�Љ�̃��[����펯�ɓ���ނ��Ƃ��ł��Ȃ��l���o�Ă���̂��܂����R�ł��B
���̂悤�Ȑl�����́A���ʂ̐l�ԊW��z���Ȃ��Ȃ�����Љ�ɏ������邱�Ƃ�����ɂȂ����肵�āA�������Ƃ����ł��Ȃ��Ȃ����肵�܂��B
�ł��̂ŁA���������l�������~�ς���d�g�݂��K�v�ɂȂ��Ă���̂ł����A���{�ɂ͂قƂ�ǂ��������V�X�e�������݂��Ȃ��̂��c�O�ł��B���{�ł́A���������l�������������Љ�̏펯�̕��Ɉ������荞�����Ƃ��邩�A���邢�͖�������X���������悤�ɂ������܂��B
�u��H�v�i�������ł͂Ȃ��������ł��B�j�A����́A�~�ς̎d�g�݂̂ЂƂł��B�펯�̘g�����E���Ă���i�펯�̘g�ɂƂ���Ȃ��j�l�����́A�펯�̊O���ɂ���@�i�^���ƌ����Ă��悢��������܂���j���������A���H���邱�Ƃɂ���āA��ʑ�O���瑸�h����A���肪�������āA���̑Ή��Ƃ��ĐH����������Ă���̂ł��B�C���h�Ȃǂł̓T�h�D�[�ƌĂ�܂��B
�ォ��ڐ��̑�O����H�����b��ł�����Ă���̂ł͂Ȃ��A��O���瑸�h����Ăǂ������H�ׂ��������Ƃ����킯�ŐH����������Ă���̂ł��B
��H�́A�܂�o�Ƃł���A�o���Ԃł���܂��B�o���ԂƂ́A���Ԃ̏펯�ɂƂ���Ȃ��Ő�����Ƃ������Ƃł��B
���{�̕����E�ɂ��o�ƂƂ����V�X�e���͂���܂����A���{�̏o�Ƃ́A�����Ƃ����g�D�Ɂu�]�E�v���邾���̂悤�Ȉ�ۂ�����܂��B
�Љ�ɏ����ł��Ȃ��l�����ł��A�P�v�I�ɐH������d�g�݂������������̂ł��傤���B����ȘB���p�݂����Ȃ��ƁA�����ł����ˁH
|
|
|
|
|
2011/11/23�@�B���p�����܂����B
|
|
�O��A�u�������v�̒��ŁA�u�B���p�݂����Ȃ��ƁA�����ł����ˁH�v�Ǝ��₵�Ă���A�͂��N�ȏオ�o���Ă��܂��܂����B
���̓������o���悤�ł��B
�ʎq�_�Ƌ��Z�H�w�̍l������Z������ƁA����ł̘B���p�����݂��邱�Ƃ��킩��܂����B
�ڍׂ͒ǂ��āA���̃z�[���y�[�W�̒��ŁA���Љ�Ă䂫�܂��B
|
|
|
|
|
2011/12/20�@�B���p�l�i���̂P�j
|
|
�B���p�̃q���g�́A�J�W�m��ی���Ђ̎d�g�݂Ɍ��Ď��܂��B
�J�W�m�́A���w�҂��ق��āA�J�W�m������L���ƂȂ�悤�ȃQ�[����p�ӂ��܂��B
�Ⴆ�A���[���b�g�ɂ�38�̃|�P�b�g������A1����36�܂ł̐��������蓖�Ă�ꂽ�Ԃƍ���18���̃|�P�b�g�ɉ����āA�u0�v�Ɓu00�v�̗̃|�P�b�g������܂��B
�Ԃ�10�h���q����A�Ԃ̃|�P�b�g�Ɏ~�܂����Ƃ���10�h���̔z�������炦�A�����Ɏ~�܂����Ƃ��ɂ�10�h�������܂��B
���̃Q�[���̏����́A�Ԃ̃|�P�b�g��18�Ȃ̂ŁA18/38=0.473�B
�z���̊��Ғl�́A10$�~18/38-10$�~20/38=-0.526$�B
�M�����u���[�̏�����5�����Ⴂ���A�z���̊��Ғl���}�C�i�X�ł��B
�����ł��A�M�����u���[�́A���[���b�g������邽�тɕ���52�Z���g����������悤�ɂł��Ă���̂ł��B
�������M�����u���[�����ۂ�52�Z���g�������Ƃ͂Ȃ��A����10�h�������A10�h�������邩�̂ǂ��炩�ł��B
�Ƃ͂����A���x�����x�����̓q�����J��Ԃ��A�M�����u���[�͕��ςŖ���52�Z���g�������ƂɂȂ�̂ł��B�������āu�吔�̖@���v�̋]���҂��܂���l������킯�ł��B
�J�W�m�͕s���A�����Ă��̖@�����J�W�m��K��閳���̃M�����u���[�ɓ��Ă͂܂�܂��̂ŁA�J�W�m���ɂ͔���ȗ��v���ۏႳ���̂ł��B
�ی���Ђ��J�W�m�Ɏ��Ă��܂��B�ی���Ђ́A�l�̎��ʊm���⎖�̂̋N����m����Ȗ��Ɍv�Z���Ă��܂��B
�����āA���ۂɐl�����Ƃ��⎖�̂��N�������Ƃ��Ɏx����Ȃ���Ȃ�Ȃ��ی��������\�������̂����������Ă���悤�ɕی��������߂Ă���̂ł��B�ی������҂͖����ɂ���̂ŁA�����������Ƃ��\�ɂȂ�܂��B
���N�Ŏ��̂ɂ���Ȃ��l�̂ق������|�I�ɑ����̂ŁA�ی���Ђ͔���ȗ��v���ۏ���܂��B
�J�W�m�ł͂��܂ɑ叟������q�����܂����A�ق��̖����ɂ���M�����u���[�̂��A�ŁA�J�W�m�����ׂ������邱�ƂɂȂ�܂��B
�ی���Ђł͂��܂ɑ傫�ȕی������x����Ȃ���Ȃ�܂��A�����ɂ���ی������҂̂��A�ŁA�ی���Ђ��ׂ������邱�ƂɂȂ�܂��B
���ꂱ�����A�u�吔�̖@���v�ƌĂ����̂ł��B
���Ȃ��́A�J�W�m�ɂȂ�Ȃ���Ȃ�Ȃ��̂ł��B
�����āA���Ȃ��́A�ی���ЂɂȂ�Ȃ���Ȃ�Ȃ��̂ł��B
���Ȃ��́A�M�����u���[�ɂȂ��Ă͂����܂���B
�����āA���Ȃ��́A�ی������҂ɂȂ��Ă͂����Ȃ��̂ł��B
���K���܂��傤�B
�B���p�̃L�[���[�h�́A�u�����v�A�u���Ғl�v�A�����āu�吔�̖@���v�ł��B
�����āA�l���J�W�m��ی���ЂɂȂ���@�������Ȃ���Ȃ�܂���B
����Ȃ��܂����@������̂ł��傤���H
���͂���̂ł��B
�i���B�j
|
|
|
|
|
2012/1/7�@�B���p�l�i���̂Q�j
|
|
�O�[���b�g�́A������5���ȉ��Ŋ��Ҏ��v�����}�C�i�X�ł���A�Ƃ������b�����܂����B
����ł́A����FX�i�ב֏؋�������j�͂ǂ��ł��傤���H
���Z�H�w�ł́A����בւ͌����Y�ƌĂ�A�����Y�̉��i�̓u���E���^���Ń��f��������܂��B
�ʎq�͊w�Ō����A�d�q�Ɠ����ł��B
�d�q���A�S�������_���ȓ���������̂Ɠ����悤�ɁA������בփ��[�g���S�������_���ɏ㉺���܂��B
�܂�A����������ב֎���Ƃ��������i�̕����ɓq���邱�̃Q�[���́A����������T������ʂ����T�A�Ƃ������ƂŁA��������͂������t�B�t�e�B�[�E�t�B�t�e�B�[�Ȃ̂ł��B
���i���オ��m����50%�A������m����50%�ł��̂ŁA������5���Ƃ������ƂɂȂ�܂��B
�����āA������5���Ƃ������Ƃ́A���̃Q�[�������x�����x���J��Ԃ��A���������Ȃ��Ƃ������ƂɂȂ�܂��̂ŁA���Ғl�̓[���ł��B
���[���b�g�́A������5���ȉ��Ŋ��Ҏ��v�����}�C�i�X�ł���܂�������A����בււ̓����̓��[���b�g���͂܂��A�Ƃ������Ƃł����A����בւ͏���5���Ŋ��Ғl�̓[���ł�����A�������Ă����͑S�����ɂȂ�Ȃ��̂ł��B
����בւŋ��R�����Ƃ����܂ɂ͂���ł��傤�B�����Œ��q�ɏ���Ă�����x���ƍ��x�͑����āA�O�ׂ̖����������ł��܂��A�Ȃ�Ă��Ƃ��悭����܂��B
���ꂪ�吔�̖@���ł��B�܂�吔�̖@������͓�����Ȃ��̂ł��B
�R�C����10�炢�����������ł́A�\��7��o�ė���3��Ȃ�Ă��Ƃ�����܂����A�ꖜ���Ă݂�A�\�܂��͗��̏o�銄����5���Ɍ���Ȃ��߂Â��Ă��܂��B
����בւ������ł��B�����قǏ���5���A���Ғl�[���ɋ߂Â��Ă䂫�܂��B�܂�ׂ���Ȃ��̂ł��B
����בւ�����Ă������������A��������߂Ă��܂��̂������ł��B
�J�W�m�ł����܂ɑ叟�����邱�Ƃ�����܂��B���̑̌��ɖ������߂ĉ��x������Ă��܂������ʁA�呹���������A�Ȃ�Ă����l�����܂����ˁB
������吔�̖@���̋A���ł��B�Ȃɂ��J�W�m�̓M�����u���[�����s���Ȃ悤�ɂł��Ă���̂ŁA�����قǑ������c���ł���̂ł��B
�ׂ��邽�߂ɂ́A����5���ȏ�A���Ғl���v���X�łȂ���Ȃ�܂���B�u����v�͈�̉��Ȃ̂��H
���Ă����悤�ɁA������בւ̓����͑S���\�z�ł��Ȃ��Ƃ����̂����Z�H�w�̋A���ł��B
�ł��̂Łu����v�͊���FX�ł͂���܂���B
����בւƓ����悤�ɁA�ʎq�͊w�ł͓d�q�̓����͑S���\�z���邱�Ƃ��ł����A�V�����f�B���K�[�������ŗ\���ł���̂͗B��A�g���������ł���܂����B
�ł́A�ʎq�͊w�Ō����Ƃ���̔g�����̂悤�ɁA�\���\�Ȃ��̂����Z�̐��E�ɂ͑��݂���̂ł��傤���H
���͑��݂���̂ł��B�����Ă��̏����́H�A���Ғl�́H
�i���B�j
|
|
|
|
|
2012/1/21�@�B���p�l�i���̂R�j
|
|
���āA�O��͊���בւ͌��ǖׂ���Ȃ��Ƃ������b�����܂����B
����בւ̓����_���ɏオ�����艺�������肷��̂ŁA���x���������J��Ԃ��Ƒ吔�̖@���ŁA���v�̊��Ғl�̓[���ɂȂ��Ă��܂�����A�Ƃ����b�ł����B
�܂�A�ׂ���Ȃ������́A������בփ��[�g�̓����������_���ł���Ƃ������ƂȂ̂ł��B
�����_���ɓ����̂ŁA�����̉��i���\�z�ł��Ȃ��ƌ��������邱�Ƃ��ł��܂��B
����ł́A���̃����_�������������邱�Ƃ��ł���A�ׂ�����̂ł��傤���B
�����Ȃ̂ł��A�ׂ���̂ł��B
�����I�A�ł��ǂ�����ă����_���ȓ������������Ƃ��ł���́H
�ƊF����͎v����ł��傤�B
������בւ́A�吨�̓����Ƃ��������蔄�����肵�Ă���̂ŁA�����_���ɏ㉺���܂��B
����Ȃ��̂��������ƂȂ�Ăł��Ȃ�����āB
���ʂ��炨�b���܂��ƁA����́A��̋��Z���i���������킹���邱�Ƃɂ���ĉ\�ɂȂ�܂��B
���Z���iA�������Ɖ��l���Ȃ����A���Z���iB�����ł����l������܂���B
�ł����Z���iA�Ƌ��Z���iB���������킹�邱�Ƃɂ���āA�����_�����������āA�����ɉ��l�����܂�Ă��܂��B
���l�����܂��Ƃ����̂́A�܂�A����5���ȏ�A���Ҏ��v���v���X�ɂȂ�Ƃ������Ƃł��B
���邢�́A�����_�����������Ă����ɖ@�������o�����Ƃ��ł���Ƃ������܂��B
���R�Ȋw�ł��������Ǝv���܂����A���̐��͖@�����܂���ɂ���̂ł͂Ȃ��̂ł��B
�@���͌��ʂɂ����܂���B
�����I�A�@�����܂������āA�@�������邩�炱���A�������炢�낢��Ȃ��Ƃ������ł���̂ł͂Ȃ��́H
�Ǝv�����������������Ǝv���܂����A�@���Ƃ����̂́A���܂�Ă�����̂Ȃ̂ł��B
�����āA�����琶�܂�Ă��邩�Ƃ����A�V�����f�B���K�[���u�����Ƃ͉����v�̒��Ō����Ă����悤�ɁA�܂��Ƀ����_�����̒����琶�܂�Ă���̂ł��B
�܂�A���̐��̍����ɂ͂܂������_�����������āA���̃����_�����̓��v�I�Ȑ�������@�������܂�Ă���킯�ł��B
���̐��������܂����p����ƁA���R�Ȋw�����ł͂Ȃ��o�ς̐��E�ł��A�����_�����̒�����@�����ݏo����̂ł��B
�����_���ɓ������Z���iA�ƁA��͂胉���_���ɓ������Z���iB���A���郌�V�s�ɂ��������č������킹��ƁA�����ɖ@���������܂�A�\�z���\�ɂ��邱�Ƃ��ł��܂��B
���Ă̐l�X�́A���l���Ȃ��ɉ����̖�i���������킹�ċ���n�낤�Ɨl�X�Ȏ��݂��s���܂����B
�B���p�ł��B
�������A�ߋ��ɂ���ɐ��������Ƃ����l�������Ƃ͂���܂���B
�������A���̌���A���Ȃ�ʁA���Z���i�A�����ċ��Z���i�ɂ͗a������n�܂��āA���A���A�בցA�����M���AETF�AREIT�A�ב敨�A�ʊ��I�v�V�����A�����ݎA���t�����ݎA�w���敨�A�w���I�v�V�����A�w���敨�I�v�V�����A�ʉ݃I�v�V�����A�������g�A�]���ЍA���敨�A���敨�I�v�V�����A���X���I�v�V�����A���|�A����A�����A�����敨�A�����敨�I�v�V�����AFRA�A���o�����N�Ȃǂ̎d�g�A�X���b�v�A�L���b�v�A�t���A�A�X���b�v�V�����A���i�敨�A���i�敨�I�v�V�����A�V��f���o�e�B�u�ȂǂȂǁA���܂��̎�ނ�����܂����A���̒������̋��Z���i���������킹��Ƌ��Ȃ�ʁA���Ҏ��v�v���X�Ƃ������\�z�ł��A�ׂ������邱�Ƃ��ł��܂��B
���ꂪ����ŘB���p�ł��B
���Ă��̃��V�s�Ƃ́H
�i���j
|
|
|
|
|
2012/2/11�@�B���p�l�i���̂S�j
|
|
�O��́A�@������ɂ���̂ł͂Ȃ��A���G���̒�����@�������܂��̂��A�Ƃ������b�����܂����B
�����Ŗ@���Ƃ����A�j���[�g���̉^����������A�}�b�N�X�E�F���̕������A�V�����f�B���K�[�������Ƃ������A�u�������v�������@���ł��B
�ł��̂ŁA�����ł͈��Ƃ��āA���G���̒�����V�����f�B���K�[�������Ƃ����@�������܂��l�q�����Ă݂܂��B
�ł́A���̗l�q�����Ă݂܂��傤�B
�j���[�g���͊w�ł́A����dt�̊Ԃɗ��q���i�ދ���dx�Ƒ���v�Ƃ̊W�́A������݂̒ʂ�A
dx=vdt
�ł����B
�Ƃ��낪�A�ʎq�͊w�̎���ɂȂ�ƁA�d�q�̐i�ݕ��̓W�O�U�O�ŁAvdt�̂ق��Ƀu���E���^���Ƃ������G����\�������t������܂��B�܂�
dx=vdt+��dW�E�E�E�@
�ł��B�����Ń�=��(h/m)�ŁAdW���W�O�U�O�^����\���u���E���^���ł��B
���̂悤�ɓd�q�����G�ɓ����Ƃ��A�g�����Ղ�
d��=(��+v��+0.5����^2)dt+�Ѓ�dW�E�E�E�A
�̂悤�ɗ��G�ɂ�炬�܂��B�����ł��ꂼ��̋L���́A
��=id��/dt
��=d��/dx
��=d^2��/dx^2
��^2=h/m
�ł��B
�d�q�����G�A�g�������G�Ƃ������ׂƂ������E�ł��B
���Ɉȉ��̂悤�ȗʂ��l���Č��܂��傤�B
d��-��dx�E�E�E�B
�@���A�A�����A
d��-��dx=(��+0.5����^2)dt
�ƂȂ�܂��B
�����ɋC�Â��܂��H�A�����ł��A���G����\���u���E���^�������������Ă��܂��܂����I�I
d��-��dx=r(��-��x)dt
�Ȃ̂ŁA
��+0.5����^2=r(��-��x)
�ƂȂ�܂��B
r��V/h
x��0
�Ƃ��āA���A���A�Ђ̋L������̓I�ɂ���A
id��/dt+(h/2m)d^2��/dx^2=(V/h)��
�ƂȂ��āA����̓V�����f�B���K�[�������ł���܂��B
�܂�A�B�Ƃ����ʂ��l���邱�Ƃɂ���āA�d�q�����G�A�g�������G�Ƃ������ׂƂ������E����A�V�����f�B���K�[�������Ƃ����@�������܂ꂽ�킯�ł��B
�ł͇B���ł́A����������̂ł��傤���H
����́A�g���Ɠd�q���u�������킹���v�̂ł��B
�g���P�ɑ��āA�d�q-���̊����ō������킹���̂ł��B
�����̃��V�s�̗l�ɁA�g���Ɠd�q��1�F-���̊����ō��������̂ł��B
���̃��V�s�ɏ]���č������킹��ƁA������\���ł��Ȃ������ł��闐�G���������A������\�����邱�Ƃ��ł������������ɓ���̂ł��B
���āA�B���p�̘b�ɖ߂�܂��傤�B
�O��A�u�����_���ɓ������Z���iA�ƁA��͂胉���_���ɓ������Z���iB���A���郌�V�s�ɂ��������č������킹��ƁA�����ɖ@���������܂�A�\�z���\�ɂ��邱�Ƃ��ł��܂��B�v
�Ɛ\���܂����B
�����ǂ����͂����C���t���ꂽ���Ƃł��傤�B
�����ł��A�g���Ɠd�q���������킹�ăV�����f�B���K�[�������ݏo�����悤�ɁA���Z���iA�Ƌ��Z���iB���������킹�Ė@������ɂ���̂��A�u�B���p�v�Ƃ������Ƃł��B
�g���ɑΉ�������Z���i�Ƃ́H
�d�q�ɑΉ�������Z���i�Ƃ́H
�i���j
|
|
|
|
|
2012/4/21�@�B���p�l�i���̂T�j
|
|
�B���p�����܂��s�����ǂ����́A�ȉ��̎O�Ō��܂�܂��B
�����F�������^�Q�[����������
�I�b�Y�F���������̗��v�^���������̑���
�G�b�W�F�i�P�{�I�b�Y�j�~�����|�P
�����āA���ʓI�ɂ̓G�b�W���v���X�ł��邱�Ƃ��K�{�ł��B
�G�b�W�Ɗ��Ғl�́A
���Ғl�F���������̗��v�~�����|���������̑����~�i�P�|�����j���G�b�W�~���������̑���
�̊W������܂��̂ŁA���Ғl���v���X�ł��邱�Ƃ��K�{�A�ƌ��������邱�Ƃ��ł��܂��B
���[���b�g���ɂƂ��Ă݂�A�M�����u���[���́A������18/38�ŃI�b�Y��10$/10$��1�������̂ŁA�G�b�W�́|0.0526�A���Ғl�́|0.0526�~10$���|0.526$
�J�W�m���́A������20/38�ŃI�b�Y��10$/10$��1�������̂ŁA�G�b�W��0.0526�A���Ғl��0.0526�~10$��0.526$
�܂�J�W�m���ɃG�b�W�i�D�ʐ��j������A���[���b�g�̓J�W�m���ɂƂ��ĘB���p�ł��B
������90%�̃Q�[�����������Ƃ��Ă��A���������̗��v��10$�ŕ��������̑�����100$�ł���A10��̃Q�[���̂���9����90$���Ă��A�Ō�̈���100$������̂ŁA���ʂ�-10$�ł��B�܂�A
�G�b�W���i�P�{10$/100$�j�~90%�|�P���|0.01�i���Ғl�́|0.01�~100$���|1$�j
�Ƃ������ƂŁA�����������Ă��A�I�b�Y���Ⴏ��A�G�b�W�̓}�C�i�X�ɂȂ��Ă��܂��܂��B
�G�b�W���}�C�i�X�ƂȂ�̂ŁA���̃Q�[���ɗD�ʐ��͂���܂���B
�t�ɏ�����10%�����Ȃ��Ă��A���������̗��v��100$�ŕ��������̑�����10$�ł���A10��̃Q�[���̂���9���Ă�90$�����������A�Ō�̈���100$�ׂ���̂ŁA���ʂ�10$�ł��B�܂�A
�G�b�W���i�P�{100$/10$�j�~10%�|�P��0.1�i���Ғl��0.1�~10$��1$�j
�Ȃ̂ŁA�������Ⴍ�Ă����̃Q�[���ɂ͗D�ʐ�������܂��B
FX�⊔�łقƂ�ǂ̐l���ׂ���Ȃ��̂́A���̃G�b�W�Ɛl�Ԃ̃v���C�h�������ł��B
FX�⊔�͏オ��̂�������̂��t�B�t�e�B�[�t�B�t�e�B�[�Ȃ̂ŁA�����͂����炭50%���炢�ł��傤�B
���܂��ܓǂ݂��������Ėׂ����o���Ƃ��́A�������m�肵�����̂ŁA���v��L���܂���B
����ǂ݂��O��đ����o�Ă���Ƃ��́A������F�߂����Ȃ��̂ʼn��Ђ��ɂ���X��������܂��B
���̂��߃I�b�Y�i���������̗��v�^���������̑����j���Ȃ��Ȃ�1.0���邱�Ƃ��ł��Ȃ��̂ł��B
�l�ɂ���āA�I�b�Y��0.8�ł�������0.7�ł������肷��ł��傤�B
�G�b�W���i�P�{0.7�j�~50%�|�P���|0.15
�ƃ}�C�i�X�ɂȂ�̂ŁAFX�⊔�ł͌��ǖׂ����Ȃ��̂ł��B
�܂����Ƃ��A���܂߂ɗ��v���m�肵�ď����𑝂₵���Ƃ��Ă��A�����Ƃ��ɑ傫�������A��قǂ̏���90%�̗�ł��킩��悤�ɁA�G�b�W���}�C�i�X�ɂȂ��Ă��܂��̂ŁA���ǖׂ���܂���B
FX�⊔�͂�߂܂��傤�I
�G�b�W���v���X�ɂȂ�悤�ȃQ�[���������邱�Ƃ��B���p�ł��B
�G�b�W���v���X�ɂȂ�Q�[���������āA���̃Q�[������葱����A�吔�̖@���ɂ���āA���v���グ�����邱�Ƃ��ł���̂ł��B
�J�W�m��ی���Ђ͂��̃Q�[���������Ă���̂ł��B
���Z�s��i�}�[�P�b�g�j�ɂ͗a������n�܂��āA���A���A�בցA�����M���AETF�AREIT�A�ב敨�A�ʊ��I�v�V�����A�����ݎA���t�����ݎA�w���敨�A�w���I�v�V�����A�w���敨�I�v�V�����A�ʉ݃I�v�V�����A�������g�A�]���ЍA���敨�A���敨�I�v�V�����A���X���I�v�V�����A���|�A����A�����A�����敨�A�����敨�I�v�V�����AFRA�A���o�����N�Ȃǂ̎d�g�A�X���b�v�A�L���b�v�A�t���A�A�X���b�v�V�����A���i�敨�A���i�敨�I�v�V�����A�V��f���o�e�B�u�ȂǃQ�[��������܂��B
�ł̓G�b�W���v���X�Ŏ������ɂ��ł���Q�[��������̂ł��傤���H
���͂���̂ł��B�בւ⊔���Ⴀ��܂����B
�����Ă���͂��郌�V�s�ɏ]�����Q�̏��i�̑g�ݍ��킹�ł����ˁB
�i���j
|
|
|
|
|
2012/12/24�@�B���p�l�i���̂U�j
|
|
�����Ԃ�Ԃ������Ă��܂��܂��Đ\����܂���B
���͂��̊ԂɁA�B���p�����܂��������ǂ��������ۂɎ����̂������g���Ď����Ă���܂����B
��̋��Z���iA�Ƌ��Z���iB�Ƃ����郌�V�s�ɏ]���č������킹��Ƃ�����ł��B
���ʂ́A�ȉ��̃O���t�ƂȂ��Ă���܂��B
�����͉c�Ɠ����A�c���͑��v�i�P�ʂ͗Ⴆ�ΐ�~�j�ł��B
2012/5/22����͂��߂āA��T���܂ł̃O���t�ł��B
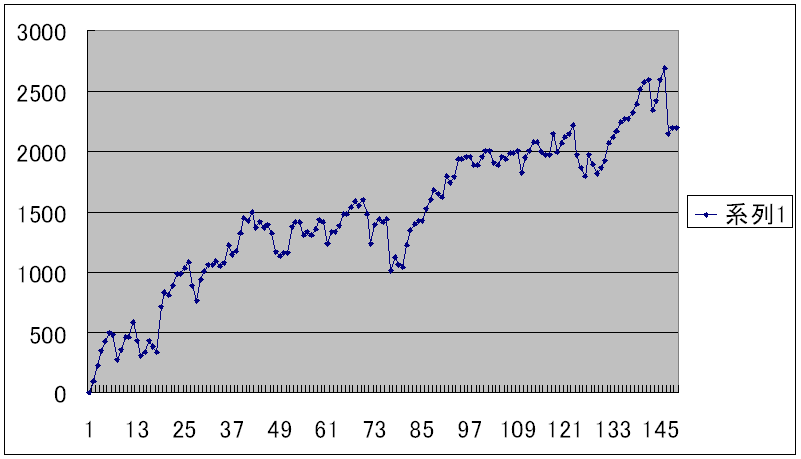
�Ƃ肠�����A���̔��N�Ԃ͂��̘B���p���@�\�����悤�ł��B
|
|
|
|
|
2013/5/20�@�B���p�l�i���̂V�j
|
|
���̘B���p�͏�_���g���Ă���B
�B���p�Ə�_�A�ꌩ�S���W�Ȃ������ł��邪�A���͑傢�ɊW������̂��B
���̂��Ƃ��ŏ��ɘ_���ɂ����̂́A1950�N��Ƀx���������œ����Ă���John Larry Kelly, Jr.�Ƃ����l�����B
�ނ��gA New Interpretation of Information Rate�h�Ƃ����_���̒��ŁA�Ȃ������n�Ə�_�̊֘A�ɂ��Ę_�����̂��B
���n�͒P�ɗ�ł����āA�M�����u���ł���Ή��ł������̂����A���Ƃ�����Ȋ����ł��遦�B
�n�̒ʂ��ԍ���i�Ƃ����B
�ni�����m����pi�ŕ\���B�i��pi = 1�j
�n���w���҂��g�������̂����A�ni�ɓ������銄����bi�ŕ\���B�i��bi = 1�j�B
�܂��A�ni�����������̔z���i���{�ɂȂ��ĕԋ�����邩�j��oi�Ƃ����B
�ni�����������̎�����������
S(i) = oibi
�ł���B
������S�̊��Ғl�ł͂Ȃ�S��log�̊��Ғl������āA
W(b) = E(log2 S(i)) = �� pi log2 oibi
�Ƃ����l���`���A�������igrowth rate�j�ƌĂԂ��Ƃɂ���B�����2�{��P�ʂƂ��������̋��x��\���l�ł���BW��1�ł����2�{�ɂȂ邵�A0�ł���Ύ����͑����Ȃ��B
�œK�Ȏ����z��b�����߂邽�߁AW(b)���ő剻���邱�Ƃ��l����B
W(b)
= ��pilog(oibi)
= ��pilog(oi(bi/pi)pi)
= ��pilog(oi) + ��pilog(pi) + ��pilog(bi/pi)
= ��pilog(oi) - H(p) - D(p||b)
�� ��pilog(oi) - H(p)
H(p)�̓G���g���s�[�BD(p||b)�̓_�C�o�[�W�F���X�i�J���o�b�N�E���C�u���[���ʁj�B�Ō�̍s�ŕs������̂Ƀ_�C�o�[�W�F���X�̔����g���Ă���BD(p||b)��0�ɂȂ�̂� b=p �̎��ł���B
���ǁAW�̍ő�l�� ��pilog(oi) - H(p) �ł���Ab=p �ɂ���Ď��������B����͂܂�A�e�n�̏��m���ɍ��킹�Ď�����z������̂��ǂ��Ƃ������ƁB
���Ƃ��Ύ㏬�̔n�����āA1/100 �̊m���ł������ĂȂ����낤�Ǝv�����Ƃ��Ă��A���̔n�ɑS�����z�� 1/100 ��q����̂��ǂ��B
���̐헪�ɂ����Ĕn���w���҂ׂ̖����ǂ�����o�Ă��邩�Ƃ����ƁA�n�̏��m���Ɣz���̊Ԃ̃Y���ł���B
�����z�������S�Ɋe�n�̏��m���f���Ă��āAoi = 1/pi �ł������Ƃ�����A
Wmax = �� pilog(oi) - H(p) = �� pilog(1/pi) - H(p) = H(p) - H(p) = 0
�ɂȂ�A�܂������ׂ���Ȃ��B
���ۂ̋��n�ł͔z�����s��ɂ���Č��܂邽�߁A��������������m�����z��\���ł����l�ׂ͖��邱�Ƃ��ł���B
���Ƃ��ΑS�n���w���҂̎�����ri�Ƃ����`�Ŋe�n�ɔz������Ă��āA���n�̎�Î҂̎�蕪���l���Ȃ��ꍇ�A�z���� oi = 1/ri �ɂȂ邪�AW(b)��ri���g���ď��������Ă݂�ƁA
W(b)
= �� pilog(bioi)
= �� pilog((bi/pi)(pi/ri))
= �� pilog(pi/ri) - �� pilog(pi/bi)
= D(p||r) - D(p||b)
���̃_�C�o�[�W�F���X�̍����������ɂȂ�B�_�C�o�[�W�F���X�͓�̊m�����z�̊Ԃ́g�����̂悤�Ȃ��́h�ƌ����邪�i���z�̌����Ɋւ��đΏ̂łȂ��̂Ő��m�ɂ͋����ł͂Ȃ��j�Ap��r�������Ap��b���߂����ɔn���w���҂ׂ̖��͑傫���B
��_�͊m���_�̈ꕔ��̂悤�ȏ�������̂ŁA������M�����u���ƌ��т��悤�ƍl����͓̂��R�̔��z�����m��Ȃ����A���̂悤�ɒ莮������Ă݂�Ɩʔ����B
���āA���ۂ̋��n�ł͋��n�̎�Î҂̎�蕪�iJRA�̏ꍇ��25%�j������B�܂��e�n�̐��m�ȏ�����\�z���邱�Ƃ��قƂ�Ǖs�\�ł���̂ŁA���̂悤�Ȃ��܂��b�ɂ͎c�O�Ȃ���Ȃ��Ȃ��Ȃ�Ȃ��B
�����ŁA���n�Ɠ����悤�ȏ��A���Z�s��̒��ō\�z���邱�Ƃ��l���Ă݂�̂��B
��̋��Z���iA�Ƌ��Z���iB�����郌�V�s�ɏ]���č������킹�����̂ł���B
���̍������i��������邱�Ƃɂ���āA�n���Q�������o������悤�ȋ��n�̏�Ԃ���邱�Ƃ��ł���B
�����Ă��̎���̏����͋��Z�H�w�̗��_�ɂ���Đ��m�ɗ\�z�ł���B
����ŏ،���Ђ�web�T�C�g������A���̎���̉��i���ڂ��Ă���B���n�̔z���i�I�b�Y�j���ڂ��Ă���̂Ɠ������B
���������ɗ�̃_�C�o�[�W�F���X�i�J���o�b�N�E���C�u���[�����j���Z�o����B
�������傫���Ƃ��ɓq��������̂��B
���n�̎�Î҂̎�蕪�͂��̏ꍇ�萔���ł���B
���Z�s��̃e���K�́A�I�����C���،��̂��̂������A���X������̂ŃM�����u���[�ɂƂ��Ă͓s�����ǂ��B
���i�Q�l�����j�@��_ -��b�ƍL����-
|
|
|
|
|
2013/7/1�@�B���p�l�i���̂W�j
|
|
�P���[�̘_���ɂ��đ�ς킩��₷��������Ă��������Ă���T�C�g������܂����̂ŁA����͂��̃T�C�g�l�̋L����]�ڂ����Ă��������܂����B
******************************************************************************
���̂悤�ȃM�����u���ɂ��čl���܂��B
�吨�̐l�œq���s���i���n���C���[�W���ĉ������j�B
�e�l�́AA�AB�AC �̂����ꂩ�ɍD���ȋ��z�����q����i�����ɓq���Ă��悢�j�B
�ǂꂩ�P�� �u�����v �ɂȂ�B
�q�������z�͂��ׂăv�[������A���� A ���������Ƃ���ƁAA �ɓq���Ă����l�́A�q�������z�ɔ�Ⴕ�ăv�[���������������炦��Ƃ����d�g�݂ł���B
���n�̒P���n���݂����Ȃ��̂ł����A���n�ł͍T�����������ăv�[���������z�̈ꕔ�� JRA�i���{�������n��j������Ă��܂��܂��B�����ł͍T�����Ȃ����̂Ƃ��܂��B���̉���͏d�v�ŁA�T��������ƈȉ��̘b�͐��藧���܂���B
��������܂��傤�BA�AB�AC ���ꂼ��ɑ���q�����̑��z�����̂悤�ɂȂ��Ă����Ƃ��܂��B
�@�@A�@�@�@�@�@B�@�@�@�@�@C
100���~�@200���~�@300���~
�q�������v�[���������̂́A600���~�ł��ˁB
���� A �������ɂȂ�A100���~�ɑ��A600���~�����炦�銨��ł�����A�{���� 6�{�Ƃ������ƂɂȂ�܂��B�܂�AA �� 200�~�q���Ă����l�� 1200�~�߂��Ă���킯�ł��i�ׂ��� 1000�~�j�B
���l�ɍl���āAB �̔{���� 3�{�AC �� 2�{�ł��B
���āA���Ȃ��́A���̐l���q����̂�����߂���A�Ō�ɓq���邱�Ƃ��ł���Ƃ��܂��B
A�AB�AC �Ɍ����_�œq�����Ă�����z��m������œq���邱�Ƃ��ł���킯�ł��B
�܂��A���̂��Ƃ����肵�Ă����܂��B
���Ȃ��͏��z�ł����q���Ȃ����߁A���Ȃ��̓q�����ɂ��{���̕ω��͖������Ă悢�B
���Ƃ��A��̗�̂悤�ȏ���A���Ȃ��� A �ɐV���� 100�~�q����Ƃ��܂��B�{���Ȃ�A���Ȃ����q���邱�ƂŁAA �ɑ���q�����̑��z�� 1000100�~�ɂȂ�܂��B����́A�킸���� A �̔{���������AB�AC �̔{�����グ��͂��ł��B�������A���̔{���̕ω��͂킸���Ȃ̂ŁA�ȉ��A�{���͕ς��Ȃ��Ƃ��čl����Ƃ������Ƃł��B
���̉���͕K�������K�v�ł͂Ȃ��̂ł����A�ʓ|�Ȃ̂ł������Ă����܂��B
����ƁA���̎������������Ă����ĉ������B����́A�T�����Ȃ����߂ɋN���邱�Ƃł��B
���Ȃ��͎����̂��ׂĂ��AA�AB�AC �̂��ꂼ��ɔz�����ēq����Ƃ��Ă悢�B
�܂�A�L���b�V���E�|�W�V�����̓[���Ƃ��Ă����̂ł��B
���R�͊ȒP�ł��B��قǂ̗�Ő������܂��傤�B
���� 600�~�̎������AA �� 100�~�AB �� 200�~�AC �� 300�~�Ɣz�����ēq����Ƃ��܂��B���̏ꍇ�A���ʂ��Ȃ�ł���A���Ȃ��ɂ� 600�~���߂��Ă��܂��B�܂�A�q���Ă��Ȃ��̂Ɠ����Ȃ�ł��ˁB
�]���āA���Ȃ��̎����� 1000�~�ŁAA ��400�~�q���A�c��� 600�~�͌����Ŏ����Ă������Ȃ�A���� 600�~�� 100�~�A200�~�A300�~�ɕ����āAA�AB�AC �̂��ꂼ��ɓq���Ă��������ł��B
���ǁA�uA �� 400�~�A600�~�͌����v �Ƃ���̂ƁA�uA �� 500�~�i400�~+100�~�j�AB �� 200�~�AC �� 300�~�v �Ƃ���͎̂����I�ɓ����ł��B
��ʂɁAA�AB�AC ���ꂼ��̓q�����̑��z�ɔ�Ⴗ��悤�Ɏ����z��������A�����Ŏ����Ă���̂Ɠ����ł��B
���̂��߁A�L���b�V���E�|�W�V�����͕s�v�Ȃ̂ł��ˁB�ȉ��A�˂Ɏ莝�������̂��ׂĂ�q����Ƃ��܂��B
�ł́A���B���Ȃ��́AA�AB�AC �̂ǂꂪ�����ɂ��Đ��m�Ȋm����m���Ă���Ƃ��܂��B
���܁A������A20���A30���A50���Ƃ��܂��傤�B���݂̓q�����̑��z�A�{���A�������܂Ƃ߂��̂����̕\�ł��B
�@�@�@�@�@�@�@�@�@�@�@�@A�@�@�@�@�@B�@�@�@�@�@C
�q�����̑��z�@100���~�@200���~�@300���~
�{���@�@�@�@�@�@�@�@�@6�@�@�@�@�@3�@�@�@�@�@�@2
�����@�@�@�@�@�@�@�@�@20���@�@�@30���@�@�@�@50��
���̃Q�[���͉���ł��ł�����̂Ƃ��āA�P���[����g���܂��傤�B
���Ȃ��́A���� 1000�~�����Ă���Ƃ��܂��B�ǂ̂悤�ɓq����̂��悢�ł��傤���H
�P���[��ɏ]���āA���Y�̑ΐ��̊��Ғl���ő�ɂ���q���������߂�ƁA
A �� 200�~�AB �� 300�~�AC �� 500�~
�Ƃ�����ɓq����̂��œK�ƂȂ�܂��i�v�Z�ߒ��͂킩��Ȃ��Ă��\���܂���j�B
���āA�����܂ł��A�O���ł��B���悢��{��B
���݂̓q�����̑��z�A�{���A���������̕\�̂悤�ɂȂ��Ă�����ǂ����܂����H
�@�@�@�@�@�@�@�@�@�@�@�@A�@�@�@�@�@B�@�@�@�@�@C
�q�����̑��z�@300���~�@200���~�@100���~
�{���@�@�@�@�@�@�@�@�@2�@�@�@�@�@3�@�@�@�@�@�@6
�����@�@�@�@�@�@�@�@�@20���@�@�@30���@�@�@�@50��
��قǂ̕\�Ɣ�ׂĉ������B�����͓����ł��ˁB
�Ƃ��낪�A�Ȃ�ƁA�����Ƃ������₷�� C �ɐl�C���Ȃ��A���{���ƂȂ��Ă��܂��B
����A���Ă錩���݂̏��Ȃ� A ���l�C�Œ�{���B
���̎Q���҂����́A�傫���ǂ݊ԈႦ�Ă���킯�ł��ˁB���Ȃ��ɂƂ��ẮA�`�����X�ł��I
���R�A��قǂ̏ꍇ�ɔ�ׂāA
C �ɑ���q�����𑝂₵�AA �ɑ���|���������炷�ׂ���
�Ǝv���ł��傤�B
�Ƃ��낪�ł��B�P���[��ɏ]���Čv�Z����ƁA���̏ꍇ�̍œK�ȓq�����́A
A �� 200�~�AB �� 300�~�AC �� 500�~
�ƂȂ�̂ł��B�܂�A�������Ɠ����ł��B
��ʂɁAA�AB�AC �̏����� a���Ab���Ac���Ȃ�A���������ꂼ��ɁA
a �F b �F c
�̊����Ŕz������̂��œK�ƂȂ�܂��B���������Ƃɔ{���͊W���Ȃ��̂ł��B
���̎Q���҂̓����͋C�ɂ��Ȃ��ŁA���ꂼ��̏����݂̂Ɋ�Â��Ď����z��������悢���ƂɂȂ�܂��B�����b�A�{����m���Ă���K�v����Ȃ��̂ł��ˁB
�������A���̎Q���҂��Ԉ���Ă������قǁA��ׂ������҂ł��܂��B������A���̎Q���҂��Ԉ���Ă��邱�Ƃ́A���Ȃ��ɂƂ��ă`�����X�ł���͎̂����ł��B�������A�q�����ɂ͊W���Ȃ��̂ł��B
�ǂ����āA�����������ςɔ����錋�_�ɂȂ�̂��A������������D�ɗ����Ȃ��ł��B
�L���b�V���E�|�W�V���������������o�̌�����������܂���B
�܂�A�ŏ��̗�ɂ�����œK�헪�́A
A �� 50�~�AB �� 0�~�AC �� 50�~�A���� 900�~
�Ɠ����ł��B�Q�Ԗڂ̗�ł́A
A �� 0�~�AB �� 166.7�~�AC �� 433.3�~�A���� 400�~
�Ɠ����ł��B
���Ȃ킿�A�L���b�V���E�|�W�V���������łȂ������A�܂�{�C�œq���Ă��邨���ɂ��ẮAA �����炵�AC �𑝂₵�Ă���̂ł��ˁi�Q�Ԗڂ̗�̕����L���ȓq�Ȃ̂ŁA�L���b�V���E�|�W�V���������炵�Ă���̂������I�ł��j�B
�Ƃ��낪�A�L���b�V���E�|�W�V���������̕����́A�q�����̑��z���������́i�{���̒Ⴂ���́j�ɑ����̎������`�ɂȂ�̂ŁA�����ő��E����Ă��܂��Ƃ����킯�ł��B
******************************************************************************
�ȏ�A�]���B
�P�Ԃ߂̗�́A�����������n�̃I�b�Y���Ⴍ�A�������Ⴂ�n�̃I�b�Y�������̂ŁA�Q���҂����̓ǂ݂͐^�̏����ɋ߂��̂ł����A�Q�Ԗڂ̗�ł͋t�ɏ����������n�̃I�b�Y�������A�������Ⴂ�n�̃I�b�Y���Ⴂ�̂ŁA�Q���҂����͑傫���ǂ݊ԈႦ�Ă��邱�ƂɂȂ�܂��B
�܂�A�O�b�����J���o�b�N�E���C�u���[�����Ƃ������̂��l���Ă݂܂��ƁA�P�Ԗڂ̗�ł͋������߂��A�Q�Ԗڂ̗�ł͋����������Ƃ������ƂɂȂ�܂��B
���ꂼ��̔n�̐^�̏�����m���Ă��邠�Ȃ��́A���̃J���o�b�N�E���C�u���[�����������Ƃ��A�܂�Q�Ԗڂ̗�̂悤�ȂƂ��ɓq����Α�ׂ������҂ł���̂ł��B��
�����n��̍T���������݂��邱�ƁA�����āA���ꂼ��̔n�̐^�̏�����m�邱�Ƃ͂ł��Ȃ����Ƃɂ��A��������ۂ̋��n�Ŏ��s���邱�Ƃ͍���ł��i�����A����A�O��n���i�ׂŊO��n�����o��ƔF�߂锻�����������������Ј��̕��́A����Ǝ������Ƃ�����Ă����̂�������܂��j�B
|
|
|
|
|
2013/12/31�@�B���p�l�i���̂X�j
|
|
����܂ł̘B���p�̌��ʁB
�����͉c�Ɠ����A�c���͑��v�i�P�ʂ͗Ⴆ�ΐ�~�j
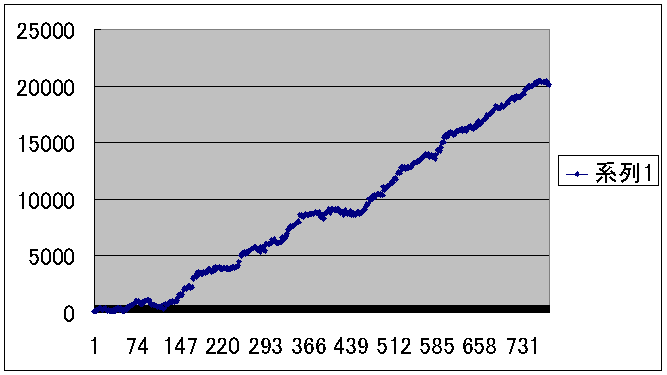
���N�̃m�[�x���o�ϊw�܂͘b����ĂB
�Ȃ����Ƃ����Ɛ^��������Η������̗��_�������Ɏ�܂������炾�B
���̓�Ƃ́A
���[�W���E�t�@�[�}�̌����I�s�ꉼ��
���o�[�g�E�V���[�̍s���t�@�C�i���X���_
�ł���B�^��������Η����Ă���̂ŁA�����ɂ͂ǂ��炩�̗��_���K���u��������_�v�ɂȂ鎖���m�������炾�B
����Ȃ킯�ŁA�u��������_����܂����A�m�[�x���o�ϊw�܁v�Ƃ������L���i���L�Q�Ɓj�����ʂ������Ă���B
���āA�{���ɂǂ��炩�̗��_�͏����쒀�����̂ł��낤���H
���͂����͎v��Ȃ��B
�u�����w�͂����ɑn��ꂽ���v�̂Ȃ��ł́A���𗱎q�ł���Ƃ���j���[�g���ƌ��͔g�ł���Ƃ���z�C�w���X�̉��z�I�ȓ��_���`����Ă��邪�A�ǂ��炩����������_�Ƃ��ċ쒀����Ă���Ƃ��������Ƃ��Ȃ����Ƃ́A���㕨���w�ł͂��łɏ펯�ɂȂ��Ă���B
�ꌩ�Η����闱�q�Ɣg���A���㕨���w�ł͗Z�����ċ������Ă���B
�u���q�Ɣg�v�ȊO�ɂ��A�u���G���Ɩ@�����v�Ȃǂ͈ꌩ�Η����邪���͋����ł���Ƃ����T�O�̂ЂƂł���B
���q�̋O���͉������猩��Ί��炩�ł��邪�A�߂Â��Ă�[�����Ă݂�ƁA�W�O�U�O�ȃ����_���ȓ��������Ă���B
�������猩��j���[�g���͊w�Ƃ����@���ɂ��������Ċ��炩�ȋO����`���Ă���悤�Ɍ����邪�A�߂��Ō���Ηʎq�͊w�I�ȗ��G�ȓ��������Ă���̂��B
�������猩��A�߂����猩��A�Ƃ����̂́A���t��ς���}�N���I�Ȏ��삩�~�N���I�Ȏ��삩�Ƃ������Ƃł���A�X�P�[����ς��Ă݂�Ɠ������̂��قȂ錩����������Ƃ������Ƃł���B
���C�A�[�Y�E�|�[�J�[�̒��ɁA�u�����ڂŌ���ƁA�s�ꂪ��{�I�Ȍo�ϖ@���œ����Ă��邱�Ƃ͂܂������Ȃ��B
���A�Z���I�ȃJ�l�̗���͂���قǗ��ɂ��Ȃ������̂ł͂Ȃ��B�v�Ƃ��������肪����B
���̂�����͎����I�ł���B�����̎��ԃX�P�[���Ń}�[�P�b�g�����Ă݂�Ύs��͌����I�ł��邪�A�Z���̃X�P�[���Ō��Ă݂�ƃ}�[�P�b�g�͔�����I�A�܂�s���t�@�C�i���X���_�ɋ߂��Ƃ����킯�ł���B
�ꌩ�Η����邩�̂悤�Ɍ�����A�����I�s�ꉼ���ƍs���t�@�C�i���X���_�ł��邪�A���Ԃ̃X�P�[����ς��Ă݂�Ɠ������̂�����������������Ă��邾���Ȃ̂ł���B
�����āA�s���t�@�C�i���X���_�ƌ����I�s�ꉼ�����������Ă���}�[�P�b�g�ɂْ͍�@��i�A�[�r�g���[�W�j�����݂��A�ڂ����͏����Ȃ������ꂱ�����B���p�̌����Ȃ̂ł���B
*********************�@��������_����܂����A�m�[�x���o�ϊw�܁@******************
�m�[�x���o�ϊw�܂ƁA�o�ϊw�̂Ȃ�
���N�̃m�[�x���o�ϊw��҂����肵���B�ăV�J�S��̃��[�W���E�t�@�[�}�A���[�X�E�s�[�^�[�E�n���Z���A�����āA�ăG�[����̃��o�[�g�E�V���[�̂R���̋�����܂ƂȂ����B��ܗ��R�́A���Y���i�̌���v���̎��ؓI���͂��B����̃m�[�x���o�ϊw�܂͉���I�ł���B������܂߂āA�|�C���g�͂R����A���ԂɌ��Ă������B
�x��������A�m�[�x���܈ψ���
���ɂ́A��������_���m�[�x���܂���������Ƃ��m���ɂȂ������Ƃł���B
3�l��������܂ƂȂ������R�̂ЂƂ́A���Y���i�̌���v���͌o�ϊw�҂ɂ͂킩���Ă��Ȃ����Ƃɂ���B�o�ϊw�҂ɂ킩���Ă��Ȃ����Ƃ̌������m�[�x���܂ɂȂ�킯������A�����≻�w�̊w�҂��炵���瑲�|���̂��낤���A���ꂪ�o�ϊw���B
���̃R�����ł��U�X�w�E�����Ƃ���A�����̊�����בւ́A�t�@���_�����^���Y�ƌĂ����́A����������A��ƋƐт�����Ȃǂɂ�茈�܂�킯�ł͂Ȃ��B�������A���W�Ƃ������Ȃ��B���̂悤�Ȍ����̒��ŁA������בւȂǂ̋��Z���Y�̎s�ꉿ�i�����̎��Y�̃��X�N�ƃ��^�[���Ƃ����t�@���_�����^���Y�łقƂ�ǂ��ׂĐ����ł���Ǝ咣��������t�@�[�}�ƁA����ɋ^���悵�A����A�^�������甽�_�������Ă���V���[�������Ɏ�܂���̂ł��邩��A�ǂ��炩�͕K���Ԉ���Ă��邱�ƂɂȂ�B�ǂ��炩���K���ԈႢ�ƂȂ邱�Ƃ����m�ŁA�m�[�x���܂�^�����A�����A���S�Ɍ�����咣�����������w�҂��m�[�x���܂�������Ă����Ƃ������Ƃ��N���邱�Ƃ�100���m���Ȓ��ŁA��l�ɏ܂�^���邱�Ƃɂ����̂�����A�m�[�x���܈ψ�����x��������B
�t�Ɍ����A���ꂪ�o�ςƌo�ϊw�̌����ł���A���R�Ȋw�Ƃ̑傫�ȈႢ���B
����ɂ͂R�̗��R������B���ɂ́A�o�ϊw�͖��n�Ȋw�₾�Ƃ������Ƃ��B�o�ϊw�ɂ́A�o�ς̂��Ƃ͂܂������킩���Ă��Ȃ��̂��B���Y���i�̕ϓ��̗��R�́A�킩��Ȃ��B���Ȃ��Ƃ��w��I�ɂ͊m���������_�A�������@�͂Ȃ��B�����ŁA����̃m�[�x���܂́A�����_�ł̂Q�̗L�͐��̂��ꂼ��̑�\�A�����I�s�ꉼ���𒆐S�Ƃ�������t�@�C�i���X���_�̃t�@�[�}�ƁA�����ƍs�������ׂĂ����߂�s���t�@�C�i���X���_�̃V���[�������Ɏ�܂��邱�ƂɂȂ����̂ł���B
�����m��I�Ȃ��Ƃ͌����Ȃ����A�킩��Ȃ����Ƃɉʊ��ɐꍞ��ł���o�ϊw��2�̗��_����܂��邱�ƂɂȂ����̂ł���B�ʊ��ɐꍞ�ތo�ϊw�҂����������A�荞�ݑ����Ƀm�[�x���܂����ψ���̓x�����������B
|
|
|