二重スリットの実験に対する波動性からの新しい解釈
要約
電子は電子銃を出てからセンサーに当たるまで波と考える。この波は実験装置の構造上次の二つの現象が起こる。
１．干渉 ２．フランウンフォファー回折
この二つの現象が合わさって、最終的にセンサーにかなり鋭い波形がぶつかりセンサー面を輝かせる。この事実と装置のフィラメントがつくるポテンシャルの「ゆらぎ」によって、輝点がランダムに現れる実験結果を説明できる。つまり一切は波動現象で、電子と言う粒子は考えない。
１. はじめに
かつてリチャード・ファインマンは自然の本質が粒子性と波動性の両方を示す二重スリットの実験は量子力学の真髄であり、唯一のミステリーであると言った。
日立基礎研究所の外村ら1は思考実験しかできないといわれていた電子での二重スリットの実験を実際に行った。
現在この実験はコペンハーゲン解釈で説明されている。
外村らはこう書いている：
According to the interpretation in quantum mechanics, a single electron can pass through both of the slits in a wave from called “probability amplitude” when the uncertainly of the electron position in the wall plane covers the two slits, and when no observation is made of the electron at either one of the slits. The electron is then detected as a particle at a point somewhere on the screen according to the probability distribution of the interference pattern.1
これが所謂コペンハーゲン解釈である。
この研究の目的は、この実験を波動性のみから説明することである。私たちの研究は、シュレディンガー方程式の波動関数が確率振幅ではなく、実際の波であるという点でコペンハーゲン解釈とは異なる。
2.外村らによる日立基礎研究所の二重スリットの実験の理論1
→ 外村論文からの抜粋
The biprism consists of two parallel
grounded plates with a fine filament between them, the latter having a positive
potential relative to the former. The electrostatic potential is given by 
and the incoming
electron wave by 
, the deflected wave is given by
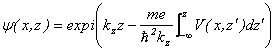, (1)
The two waves having passed on each side of the filament can be approximated by
up to a constant
factor, where
, (2)
and the symmetry 
has been taken
into account.
This can be interpreted classically also:
is the 
component of
force exerted on the electron. Its integral with respect to 
(
) gives the impulse imparted to it, which is the same in
absolute value but reversed in sign, depending on which side of the filament
the electron passes.
If the two waves overlap in the observation plane to give
, (3)
then this leads to the interference fringes
. (4)
外村論文からの抜粋 ←
コペンハーゲン解釈では、
は確率振幅であると結論付けている。
3.コペンハーゲン解釈ではなく波動性のみからの説明
外村論文の（２）式と（３）式の間の文章の中の
、
より、
を消去すれば、
となる。
この式を外村論文の（１）式に代入すれば、
となる。
また外村論文の（２）式は
となる。
しかし、正確には、前回の論文2の⑱、⑲で求めたゆらぐ波動を使わなければならないので、
電子が受ける力積は
ではなく、
.
である。（⑱や⑲では入射方向が、力を受けて電子が曲がってゆく方向が
であったのに対し、外村らの実験では、入射方向が
、力を受けて電子が曲がってゆく方向がであることに注意。）
これが、ゆらぎの原因である。力積のゆらぎによって電子の運動量がゆらぎ、電子の波数ベクトルがゆらぐ。そして⑱、⑲をみるとわかるように、波はポテンシャルの中にいるときだけゆらぎの影響を受け、ポテンシャルが事実上ゼロとみなせる領域では波はゆらがない。
よって、
はバイプリズムから出てきた波ごとに異なった値になる。
（２）式は、バイプリズムに入る電子波が、バイプリズムの出口に到達するまでに受ける影響の集積でが決まる事を意味するが、力積がゆらいでいるため、第一波がバイプリズムの中で受けた影響と、第二波が受けた影響とでは、一般に異なることになる。この結果、それぞれの波によっての値が異なることになる。
外村論文の（３）式
に示されているように、左右のバイプリズムからスクリーン上に到達する波動にも、が入っているので、力積のゆらぎの影響を受けて、位相がゆらぐことになる。
波数がゆらぐときの干渉の様子を以下に見てみる。
外村論文の（３）式により、左からくる波の波数ベクトルは
、右からくる波の波数ベクトルは
。
力積が左右対称にゆらがないため、左からのと右からのは一般に等しくない。そこで、左からくる波の波数ベクトルを
、右からくる波の波数ベクトルを
とそれぞれ書く。（
のみあるいは
のみに着目してみても、第一波、第二波、第三波･･･で、異なる値になる。）
図１．左からくる波数と右からくる波数が等しい場合
輝点は、スクリーンの中央に現れる。
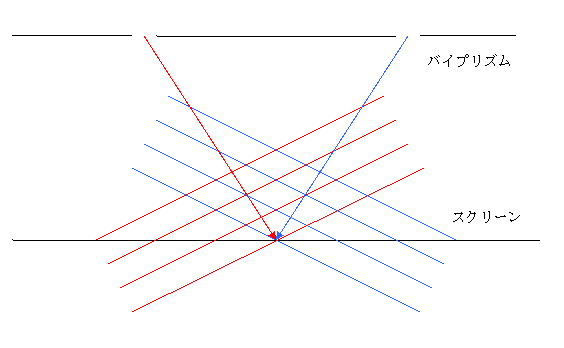
図２．左からくる波数より右からくる波数の方が大きい場合
輝点は、左側にずれる。
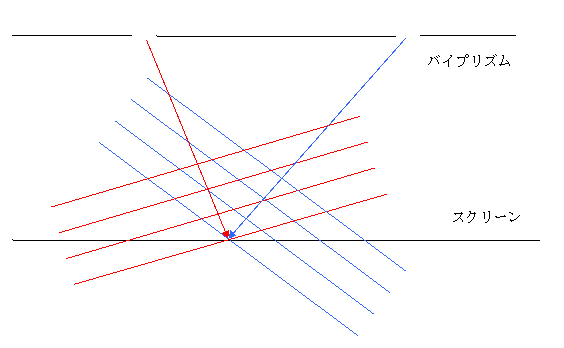
図３．左からくる波数より右からくる波数の方が小さい場合
輝点は、右側にずれる。
これが、ランダムな位置で観測される仕組みであると思料。
フィラメントが作るポテンシャルの中で受ける力積がゆらいでいるため、左のプリズムを通ってくる波の波数と右のプリズムを通ってくる波の波数は、ゆらぎの影響で大きくなったり小さくなったりする。その結果、上図のように二つの波が強めあう位置がその時々によって異なることになる。
現在の量子論では、図１の場合のみを考慮しており、以下の図で丸をつけたところが干渉縞の位置であるといわれている。
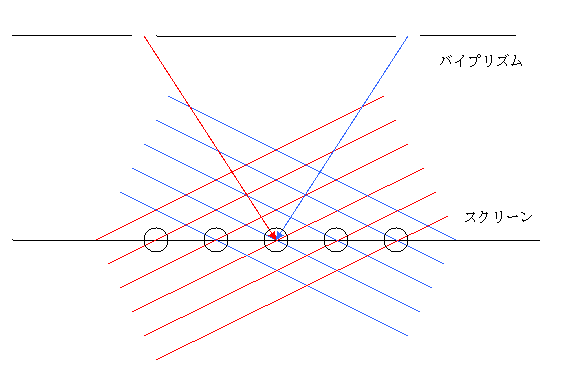
現在の量子論のものは非常に静的なイメージである一方、今回の考察では、動き回る二本のサーチライトが独立して夜空に光の波を振り撒いているように、とても動的なイメージになるので、私たちの解釈は量子論の解釈と異なる。
次に、電子波を弱くしていったときに、実験では何故、輝点として観測されるのかを考えてみる。
実際の実験では、バイプリズムの開口部がデルタ関数のような理想的なものではなく、有限の大きさを持っているため、上記の干渉効果にさらに回折効果が加わる。（所謂、フラウンホーファー回折。）
このため、スクリーン上の電子波の強度は、
関数で表される干渉縞を
関数（
）で絞り込んだ形になる（下図参照。数値の一部は外村論文より抜粋）。
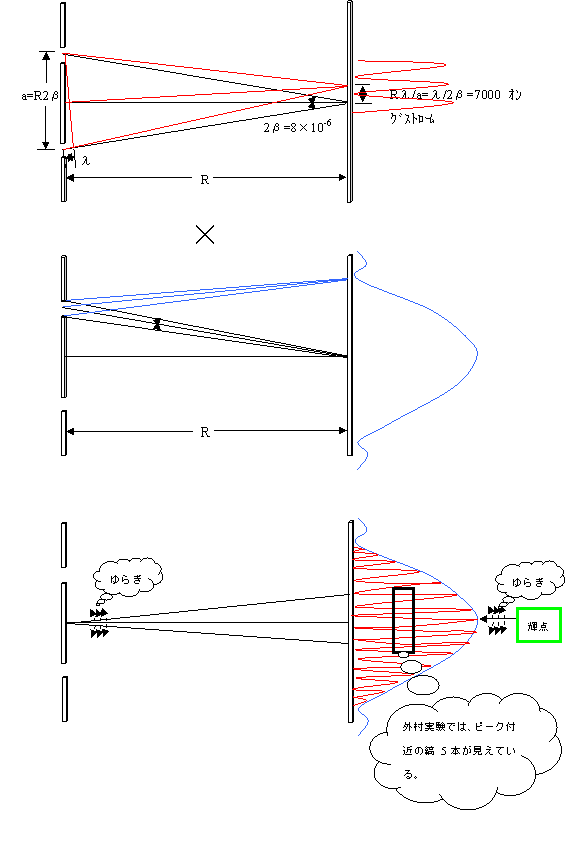
スクリーン上の電子波の強度は、山をスライスしたこの形状になる。
さらに実験では、ぎりぎりの感度で撮像しているため、山頂のごく狭い領域（所謂、エアリーディスクの中心部）のみが映ることになる。これが、スクリーン上で観測される輝点であると思料。
そしてこの山頂が前述のゆらぎによって、ランダムにゆれる。
場がゆらぎ、電子波がゆらぐため、フラウンホーファー回折の分布のピークがランダムに現れる。そして、電子銃から放出される電子波が弱いため、ピークの部分だけが造影される。
以上が、二重スリットの実験で、ゆらぎを考慮することによる波動性のみからの説明である。
4.実験への提言
今回の私たちの提案では、あの図のピークが撮像されているだけであり、それがゆらいでいるので、恐らく十数本程度しか干渉縞が撮影されないはずである。
ざっくりとした概算は以下の通りである。
フラウンホーファー像のピークの位置のゆらぎの標準偏差（ボラティリティー）は、⑲より
である。
外村らによれば、
スリットからスクリーンまでの距離：
電子の速度：
（加速電圧：
）
は約0.8マイクロメータとなる。
よってフラウンホーファー像のピークの分布する範囲は、1（68%のカバー率）で
マイクロメーターである（×２は正規分布の両側の意味）。
従って干渉縞の数 = 1.6マイクロメーター ÷900オングストローム = 18本
となり、十数本くらいしか干渉縞は撮影されないはずである。
また、フラウンホーファー像のピークのゆらぎは正規分布であるので、中心部の干渉縞が明るく、周辺にかけて暗くなると予想される。
5.結論
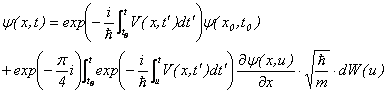
この解の存在によって、波動関数そのものがゆらぐ。この新しいシュレディンガー方程式の解を使えば、外村らによる日立基礎研究所の二重スリットの実験の結果を以下のように説明できるのではないかと私は期待している。
二重スリットの実験では、バイプリズムから出るそれぞれの波の波数ベクトルが正規分布でゆらぐ。
バイプリズムを出た波はこのゆらぎのために、さまざまな方向に発射される。
このゆらぎは、正規分布という確率分布で、規定される。
現在の量子力学では、電子の存在確率分布を決めているのは波動関数であるとされているが、今回の考察では、確率分布を決めているのは、波動関数ではなく、この運動エネルギーの指数関数部分である。これにより実体としての波動そのものがゆらぐのである。
そして、スクリーン上で観測される輝点は、「電子」ではなくフラウンホーファー回折像のピークである。
参考文献
1A.Tonomura, J.Endo, T.Matsuda, T.Kawasaki, and H.Ezawa, Demonstration of single-electron buildup of an interference pattern, [ American Journal of Physics 57 (1989), 117-120]
2Y.
Kishi, S. Umehara, Alternative method to solve the Schrodinger equation and its
solution, [XXX 99 (YYYY), 999-999]