�V�����f�B���K�[�������̐V������@�Ƃ��̉�
�v��
�V�����f�B���K�[�������̐V������@�o�����B���̉��͔g������炢�ł��邱�Ƃ��������B
�]���̃V�����f�B���K�[�������̉�@�̈�ł���t�@�C���}���|�J�b�c�̌�����p������@�ł́A���Ғl�����肵�Čo�H�ϕ����s���Ă���B�{�����ł́A���Ғl�����肹���ɁA�V�����f�B���K�[�������Ƀ��[�N���b�h���̎�@���{���A������������̐��E�Ɏ����Ă��āA���Ғl���Ƃ�O�̃����_���ɓ����������߂��B�����Ă��̉���������x���[�N���b�h�����āA�ʎq�͊w�ɖ߂����B���̌��ʁA�V�����f�B���K�[�������̉��Ƃ��āA�g�����u���E���^���ł�炮�g���������o�����B
�܂��A�]���̃t�@�C���}���|�J�b�c�̌�����p������@�ł́A�g������炢�ł��邱�Ƃ͌��o����Ă��Ȃ��̂ŁA���̌����𖾂炩�ɂ����B�������Ғl�����肷��ۂɁA���Ƃ��Ƃ̔g�������L����g���̂�炬���B����邱�Ƃ𖾂炩�ɂ����B
�P. ����
���ă��`���[�h�E�t�@�C���}���͎��R�̖{�������q���Ɣg�����̗�����������d�X���b�g�̎����͗ʎq�͊w�̐^���ł���A�B��̃~�X�e���[�ł���ƌ������B
���݂��̎����͂������̉��߂Ő�������Ă���B
���̑�\�I�Ȃ��̂��R�y���n�[�Q�����߂ł���B
�������A�R�y���n�[�Q�����߂ɂ��ẮA�����g���̎��k�̃��J�j�Y�����������ł��邵�A���{�o�H�Ɗm�����z�ŋL�q�����m���ߒ��_�Ɣ�r����ƁA�m�����z�������y�ł��Ă��Ȃ��Ƃ��낪���߂Ƃ��Ă͍r���悤�Ȉ�ۂ�����B
�l���\���͊m���͊w���Ă��A�ʎq�̋O�����u���E���^���ŕ\�����邱�Ƃɐ�������(1)�B
�l���\���̊m���͊w�́A���{�o�H���l�����Ă���_�A�R�y���n�[�Q�����߂��D��Ă���Ǝv�����A�����܂ł��ʎq�̋O���ɒ��ڂ������_�ł���A���w�Ɣ�ׂ�A���w�ɑΉ�����B
���w�͔��˂���܂Ƃ��������̍s�H��������邱�Ƃ��ł��邪�A�����܂�������邱�Ƃ͂ł��Ȃ��B�����Ċ����܂��c�_���邽�߂ɂ͔g�����w���g���K�v������B
���w�ɂ����Ċ����܂�_���邽�߂ɂ͊��w�ł͏\���ł͂Ȃ��A�g�����w��p����K�v������B����Ɠ����悤�ɁA�ʎq�͊w�̓�d�X���b�g�̎����Ȃǂ̂悤�Ɋ����ۂ��L�q���邽�߂ɂ́A�m���͊w�ł͏\���ł͂Ȃ��A��͂�u�����v���K�v�ł���̂ł͂Ȃ����Ǝ������͍l�����B
���w�ɑ���g�����w������悤�ɁA�m���͊w�ɑ���u�m���g���͊w�v�̂悤�Ȃ��̂����݂���̂ł͂Ȃ����ƌl�I�ɂ͎v���Ă���B
����ŁA���ݎ�Ƃ��ėp�����Ă���V�����f�B���K�[�������̉�@�́A�o�H�ϕ��̎�@�ł���B
�V�����f�B���K�[�������̉��́A�o�H�ϕ��̎�@�ł́A�t�@�C���}���|�J�b�c�̌����Ƃ����`�ŁA�]���͕\������Ă����B
�܂�A�t�@�C���}���̌o�H�ϕ�(2)(3)�ł́A�V�����f�B���K�[�������̉���
![]() .
.
�̂悤�ɕ\�����B������
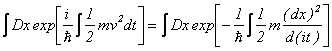
���A![]() �̒u������������Ɛ��K���z���ɑ������邱�Ƃ���A�g������
�̒u������������Ɛ��K���z���ɑ������邱�Ƃ���A�g������
![]() .
.
�Ə�����B�����ŁA![]() �́A���Ғl���Ƃ邱�Ƃ��Ӗ�����B����͏����t�@�C���}���|�J�b�c�̌����ł���B
�́A���Ғl���Ƃ邱�Ƃ��Ӗ�����B����͏����t�@�C���}���|�J�b�c�̌����ł���B
���̌����͂���Ӗ����Ғl����������Ƃ̌��ʂł���̂ŁA���Ғl���Ƃ�O�̃����_���ɓ����u�����v������͂����ƍl�����B
����́A�E�B�[�i�[�ߒ��ɂ�����u���{�o�H�v�ɑΉ�����A�u���{�g���v�̂悤�Ȃ��̂ł���B
���̘_���̖ړI�́A���Ғl����邱�Ƃɂ���ĉB����Ă��܂����A�g�����������o�����Ƃł���B
�����ŁA�V�����f�B���K�[�������Ƀ��[�N���b�h���̎�@���{���A������������̐��E�Ɏ����Ă��āA���Ғl���Ƃ�O�̃����_���ɓ����������߂��B�����Ă��̉���������x���[�N���b�h�����āA�ʎq�͊w�ɖ߂����B����ŁA�g���x�N�g�����u���E���^���ł�炮�g�����o�����B
2. �c�_
�V�����f�B���K�[������
![]() ����@
����@
�̉������[�N���b�h���̎�@�ŋ��߂邱�Ƃ��l����B���[�N���b�h���Ƃ́A�ʎq�d�C�͊w�iQED�j�̎�@�ŁA![]() �Ƃ����u���������s�����Ƃɂ���āA�ʎq�͊w�Ɠ��v�͊w���s��������Ƃ������̂ł���B���G�ȃV�����f�B���K�[�������������Ƃ��ɂ́A���[�N���b�h���ŗʎq�͊w����U���v�͊w�̌`�ɂ��ē��������߁A���̓������t���[�N���b�h���i
�Ƃ����u���������s�����Ƃɂ���āA�ʎq�͊w�Ɠ��v�͊w���s��������Ƃ������̂ł���B���G�ȃV�����f�B���K�[�������������Ƃ��ɂ́A���[�N���b�h���ŗʎq�͊w����U���v�͊w�̌`�ɂ��ē��������߁A���̓������t���[�N���b�h���i![]() �j���邱�Ƃɂ���ăV�����f�B���K�[�������̉������߂�Ƃ������̂ł���B
�j���邱�Ƃɂ���ăV�����f�B���K�[�������̉������߂�Ƃ������̂ł���B
�@�̃V�����f�B���K�[�����������[�N���b�h�����i![]() �ƒu�������j�A���ӂ�
�ƒu�������j�A���ӂ�![]() �Ŋ���ƁA
�Ŋ���ƁA
![]() ����A
����A
�ƂȂ�B
���K���z��
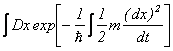
�́A![]() ��
��
![]() ����B
����B
�Ƃ����m���ߒ��ɏ]�����Ƃ��Ӗ����遦�P�B�����ŁA![]() �i
�i![]() �j�͕W���u���E���^���i�����E�B�[�i�[�ߒ��j�ł���A
�j�͕W���u���E���^���i�����E�B�[�i�[�ߒ��j�ł���A![]() �͕W�����K�m���ϐ��ł���B�i
�͕W�����K�m���ϐ��ł���B�i![]() �̒u�������ŁA�ϕ��o�H��
�̒u�������ŁA�ϕ��o�H��![]() ��
��![]() �Ƃ����������Ԃɕϊ������B����A������
�Ƃ����������Ԃɕϊ������B����A������![]() ��
��![]() �Ȃ̂ŁA���ԑ��������́A�ϕ������i
�Ȃ̂ŁA���ԑ��������́A�ϕ������i![]() �j�̋t�ɂȂ�B�܂�A
�j�̋t�ɂȂ�B�܂�A![]() �̂Ƃ�
�̂Ƃ�![]() �B�j
�B�j
�ɓ��̕�聦�Q���g���A![]() ��
��![]() �̊�
�̊�![]() �̓�����
�̓�����
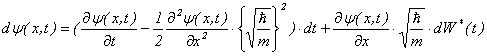 ����C
����C
�ɏ]���B�A���C�ɑ������ƁA
![]() ����D
����D
�ƂȂ�B����́A�I�����V���^�C�����E�[�����x�b�N�ߒ��ł���̂ŁA�ȉ��̂悤�ɉ������܂�(4)�B
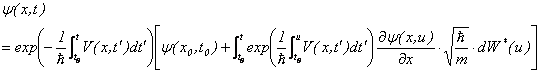
�܂��́A
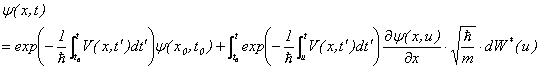 ����E
����E
�E�ӑ����炬��\���Ă���B�����ŁA�t���[�N���b�h���i![]() �j���邱�Ƃɂ���āA�V�����f�B���K�[�������̐V�������i��炮�g�����j���ȉ��̂悤�ɋ��܂�B
�j���邱�Ƃɂ���āA�V�����f�B���K�[�������̐V�������i��炮�g�����j���ȉ��̂悤�ɋ��܂�B

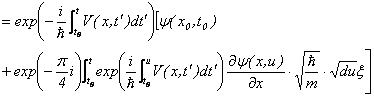
�܂��́A
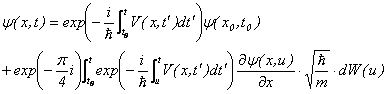 ����F
����F
�����A�V�����f�B���K�[�g���������̉��͂�炮�g�ł���B���ꂪ�V�����f�B���K�[�̔g���������̉��̐��m�ȕ\���ł���B��ꍀ�́A�|�e���V���������Ɏ��w�����ɂ���Ĕg�̎听�������Ԕ��W���Ă䂭�l�q��\���B���݂̗ʎq�_�ł͂��̑�ꍀ�������l������Ă���B������邱�Ƃɂ���Ă�炬�̌��ʂ����������B
���Ƀt�@�C���}���|�J�b�c�́A�o�H�ϕ��̎�@�ŁA���Ғl�����Ɣg�̂�炬���B����邱�Ƃ������B�����A�V�����f�B���K�[�������̐V�������i��炮���j�̊��Ғl���Ƃ�ƁA��炬������������Ă��܂����Ƃ��m�F����B
�E�̉E�ӂ�
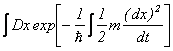
�Ŋ��Ғl���Ƃ�ƁA�E�̉E�ӑ�͈ɓ��ϕ��ɂ��![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]() ����G
����G
�ƂȂ�B�E�̑�������Ă��܂��A���̏ォ���炬�������Ȃ��Ȃ��Ă��܂������Ƃ��킩��B�G��![]() �̒u���������s���A
�̒u���������s���A
![]() ����H
����H
�ƂȂ�A�t�@�C���}���̌o�H�ϕ��i���O�����W���A���o�H�ϕ��j�Ɉ�v����B
���O�����W���A���o�H�ϕ��́A�n�~���g�j�A���o�H�ϕ�
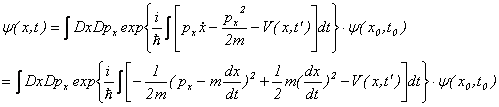
�ɂ����āA�^���ʂɊւ���K�E�X�ϕ������s�������̂����A�n�~���g�j�A���o�H�ϕ��̉^���G�l���M�[�̍�
![]()
�𐳋K���z���Ɣ�r���Ă݂�ƁA����́A�^���ʂ�
![]()
���x��炢�ł��邱�Ƃ��Ӗ�����B
�B�͍��W��
![]()
���x��炢�ł��邱�Ƃ��Ӗ����Ă���̂ŁA���̓���A
![]()
�ƂȂ�B������s�m�萫�W�ł���B
3. ��炮�g���̃C���[�W
�G���
![]() ����I
����I
�ƂȂ�B
�D�ɇI��������ƁA
![]() ����J
����J
�ƂȂ�B���ӂ�![]() �Ŋ���ƁA
�Ŋ���ƁA
![]() ����K
����K
�ƂȂ�B
![]()
�ł��邩��A�K�́A
![]() ����L
����L
�ƂȂ�B����āA
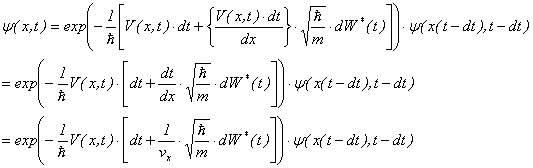 ����M
����M
�ƂȂ�B�w�����̌��Ƀu���E���^����������A����ɂ���炮�B
��d�X���b�g�̎����ɂ́A�Ⴆ�A������b�������̊O����ɂ���čs��ꂽ�d�q�ɂ�����������(5)�B�O����̓o�C�v���Y�����g�����B�ŏ��ɔނ�́A![]() �����Ɍ������ēd�q�e����d�q��ł��o�����B�����āA�ނ�̓o�C�v���Y�����g�����Ƃɂ���āA�d�q��
�����Ɍ������ēd�q�e����d�q��ł��o�����B�����āA�ނ�̓o�C�v���Y�����g�����Ƃɂ���āA�d�q��![]() �����ɋȂ��A�d�q�����������B
�����ɋȂ��A�d�q�����������B
![]() �̂悤��
�̂悤��![]() �̊��ł�����Ƃ��A���˕���
�̊��ł�����Ƃ��A���˕���![]() �ɑ��Đ����ȕ����i
�ɑ��Đ����ȕ����i![]() �����j�ɗ͂��Ȃ���Ȃ����Ă䂭�ꍇ�́A�ȉ��̂悤�ɂȂ�B
�����j�ɗ͂��Ȃ���Ȃ����Ă䂭�ꍇ�́A�ȉ��̂悤�ɂȂ�B
![]() ��d��Ƃ���ƁA
��d��Ƃ���ƁA
![]()
�ł���̂ŁA
![]() ����N
����N
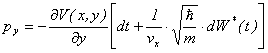 ����O
����O
![]() �����̉^���ʂ��u���E���^���ł�炮���Ƃ��킩��B
�����̉^���ʂ��u���E���^���ł�炮���Ƃ��킩��B
�M���t���[�N���b�h���i![]() �j����ƁA
�j����ƁA
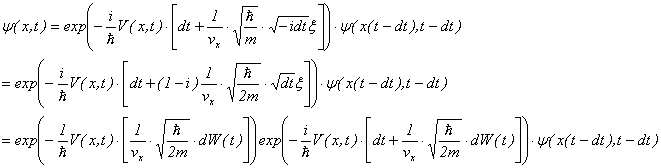 ����P
����P
�ƂȂ�B
�N�A�O���t���[�N���b�h���i![]() �j����ƁA
�j����ƁA
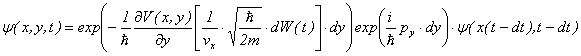 ����Q
����Q
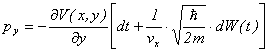 ����R
����R
�Ə�����B
�R�͗͐ς̂�炬�ɂ���ēd�q�̉^���ʂ���炮���Ƃ��Ӗ�����B���̌��ʁA�g���x�N�g������炮�B
��炮�g�ڋL�q���邽�߂ɂ́A�F��P�A�Q�����K�v�ɂȂ��Ă���B
�Ō�ɁA�{�����ɂ�苁�߂�ꂽ�V�����f�B���K�[�������̉��̈Ӗ����L���B
�t�@�C���}���̌o�H�ϕ��ł���킳���g�����́A�^���G�l���M�[�̎w���̕����ƁA�|�e���V�����G�l���M�[�̎w���̕����ɕ����邱�Ƃ��ł���B
�悭�m���Ă���悤�Ɍo�H�ϕ��̉^���G�l���M�[�����͐��K���z���ɑΉ����邱�Ƃ���A�t�@�C���}���̌o�H�ϕ��ł́A�g�����̈ꕔ���m�����z��\�����ƂɂȂ�B
�����A�g�������̂��̂��m�����z�i�m���U���j�ƍl����R�y���n�[�Q�����߂ƃt�@�C���}���̌o�H�ϕ��Ƃ͐����������Ȃ����Ƃɒ������ׂ��ł���B
�܂�A�t�@�C���}���̌o�H�ϕ��ł���킳���g�����́A�m�����z�Ŋ��Ғl���������̂��̂Ƃ������ƂɂȂ�B
�t�@�C���}���̌o�H�ϕ��ʼn^���G�l���M�[��������苎������̃|�e���V�����G�l���M�[�̎w���������́A���˔g�ɑ��ă|�e���V�����G�l���M�[�ŎU�����ꂽ�U���g��\���̂ŁA���Ғl�������O�̂��̂́A���̎U���g�ł���B
�o�H�ϕ��ɂ�����U���g�͓��Ƀ����_���ɓ����悤�Ȃ��̂ł͂Ȃ����߁A���Ғl���Ƃ邱�Ƃɂ��h�炬�����ɉB���ꂽ��̂��̂ƂȂ�B
����ŁA�{�����ɂ�苁�߂�ꂽ���́A���Ғl���Ƃ�O�̎U���g�ł���B�܂�A�g���x�N�g������炮�U���g�ł���B���̂�炮�U���g�́A���Ғl����邱�Ƃɂ���āA�B����Ă���B
�����āA�g�����̈ꕔ�ł���^���G�l���M�[�̎w���������m�����z��\�����Ƃ���A����́A�g�������̂��̂��m�����z�ƍl����킯�ɂ͍s���Ȃ��B
���݂̗ʎq�͊w�ł́A�d�q�̑��݊m�����z�����߂Ă���͔̂g�����ł���Ƃ���Ă��邪�A����̍l�@�ł́A�m�����z�����߂Ă���̂́A�g�����ł͂Ȃ��A�g�����̈ꕔ�ł��邱�̉^���G�l���M�[�̎w���������ł���B�����āA���̐��K���z�ɂ���Ċ��Ғl�������O�̎U���g�����̂Ƃ��đ��݂��A���̎U���g�͔g�����̂��̂���炮�̂ł���B
�l���\���̊m���͊w�́A�u���E���^���������������̂̂����܂ł��O���ɒ��ڂ������_�ł��邪�A�{�����́A�O�������ł͂Ȃ����̋O���ɐ����Ȕg�ʂ����g�����u���E���^��������g���͊w�ł���B
���̐V�����V�����f�B���K�[�������̉����g���A�ʎq�_�̌��������ł����d�X���b�g�̎����̌��ʂ�����ł��邪�A����͕ʕ�ɂĎ����\��ł���B
7.���_
�V�����f�B���K�[�������������V������@���o�����B
��X�́A�V�����f�B���K�[�������Ƀ��[�N���b�h���̎�@���{���A������������̐��E�Ɏ����Ă��āA���Ғl���Ƃ�O�̃����_���ɓ����������߂��B�����Ă��̉���������x���[�N���b�h�����āA�ʎq�͊w�ɖ߂����B���̌��ʔg�����u���E���^���ł�炮�g���������o�����B���̉���
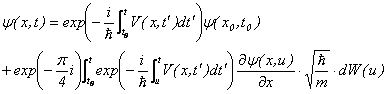
���̉��̑��݂ɂ���āA�g�������̂��̂���炢�ł��邱�Ƃ𖾂炩�ɂ����B
���݂̗ʎq�͊w�ł́A�d�q�̑��݊m�����z�����߂Ă���͔̂g�����ł���Ƃ���Ă��邪�A����̍l�@�ł́A�m�����z�����߂Ă���̂́A�g�����ł͂Ȃ��A���̉^���G�l���M�[�̎w���������ł���B����ɂ����̂Ƃ��Ă̔g�����̂��̂���炮�̂ł���B
�t�^
���P���K���z�Ɖ^���G�l���M�[
��ʓI�ɁA![]() ��
��
![]() ����@
����@
�Ƃ����m���ߒ��ɏ]�����i![]() �͕W���u���E���^���A
�͕W���u���E���^���A![]() �͕W�����K�m���ϐ��j�A
�͕W�����K�m���ϐ��j�A![]() �́A
�́A
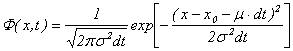 ����A
����A
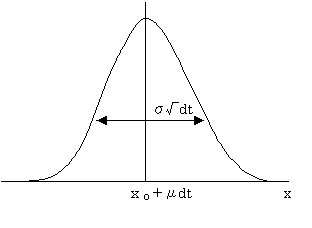
�Ƃ������K���z������B
����A�o�H�ϕ��̉^���G�l���M�[�̕��������[�N���b�h���������̂́A
![]()
�ł����A
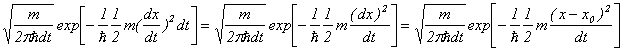 �ł��邩��A����͇A��
�ł��邩��A����͇A��
![]() �A
�A![]() �Ƃ��������̂ł���B
�Ƃ��������̂ł���B
�܂�A�o�H�ϕ��ł́A![]() ���]���ߒ��́A
���]���ߒ��́A
![]()
�ł͂Ȃ��A
![]()
�ł���B
���Q�ɓ��̕��(6)
![]() ���ɓ��ߒ�
���ɓ��ߒ�
![]()
�ɏ]���Ă���Ƃ��A![]() ��
��![]() �̊�
�̊�![]() �̓�����
�̓�����
![]()
�ɏ]���B
![]() �͕W���u���E���^����\���B
�͕W���u���E���^����\���B
�Q�l����
(1)E. Nelson, Derivation of the Schrodinger equation from Newtonian mechanics, [Physical Review 150 (1966), 1079-1085]
(2) R. P. Feynman, Space-Time Approach to Non-Relativistic Quantum Mechanics, [Rev. Mod. Phys. 20(1948), 367 - 387]
(3)R.P. Feynman, A.R. Hibbs, Quantum mechanics and path
integrals, [
(4)M. Kijima, Stochastic processes with applications to finance, [Chapman & Hall/CRC (2002), 209-210]
(5)A.Tonomura, J.Endo, T.Matsuda, T.Kawasaki, and H.Ezawa, Demonstration of single-electron buildup of an interference pattern, [ American Journal of Physics 57 (1989), 117-120]
(6)K. Ito, Memorial of the Am. Math. Soc 4(1951)