存在は本来、光なのか
「波動性と特殊相対性理論」の中で述べたように、相対論的粒子の伝播関数は、Bessel関数の漸近形を使うと、以下のような形になります。
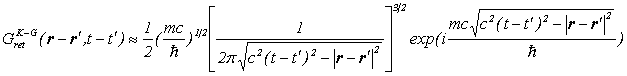
粒子の速度が遅い時には、
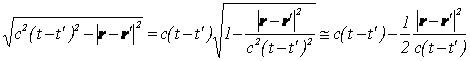
と近似できますので、指数関数の部分は、
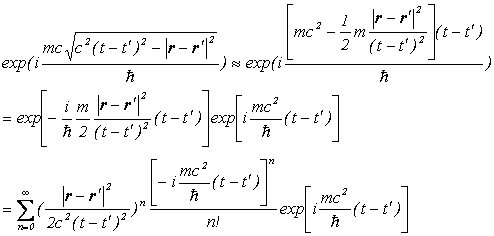 ・・・①
・・・①
となります。
①は、確率過程論での複合ポアソン過程
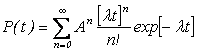 ・・・②
・・・②
の式になっていることに注目したいと思います。
ポアソン過程
![]() ・・・③
・・・③
とは、ある期間![]() の間に平均
の間に平均![]() 回起こる事象が、ちょうど
回起こる事象が、ちょうど![]() 回発生する確率を表します。
回発生する確率を表します。
損害保険の計算などで、1年間に平均300回事故が起こるとき、ちょうど121回事故が発生する確率を求めるときなどに出てくる考え方です。
そして、1回の事故で損害保険会社が支払わなければならない金額を![]() としますと、1年間に損害保険会社が支払うことになるであろう総金額を、複合ポアソン過程の式②で計算することができます。
としますと、1年間に損害保険会社が支払うことになるであろう総金額を、複合ポアソン過程の式②で計算することができます。
さて、物理の話に戻り、①式は何を表しているのでしょうか?
シュレディンガーは、電子はジグザグ運動をしているとし、これをzitterbewegungと名づけました。
そして、ファインマンは、一次元運動の電子を、光速![]() で行ったり来たりしている粒子と考えて、そこから相対論的粒子が従うKlein-Gordon方程式を導きました。
で行ったり来たりしている粒子と考えて、そこから相対論的粒子が従うKlein-Gordon方程式を導きました。
速さ![]() で走っている電子は、瞬間瞬間は光速度
で走っている電子は、瞬間瞬間は光速度![]() なのです!。
なのです!。
禅問答のようですが、速度![]() で等速直線運動をしているように見える電子は、実は光速度
で等速直線運動をしているように見える電子は、実は光速度![]() で行ったり来たりしているのです。
で行ったり来たりしているのです。
三百六十五歩のマーチのように、三歩進んで二歩さがる、のような動きを光速![]() で繰り返しており、行ったり来たりしているので、結果的にはたいした距離がすすめず、速度
で繰り返しており、行ったり来たりしているので、結果的にはたいした距離がすすめず、速度![]() で進んだという結果だけが観測されるのです。
で進んだという結果だけが観測されるのです。
以下の図でイメージしてください。
vで等速直線運動している電子の動き
(1)ニュートン力学における電子の動き
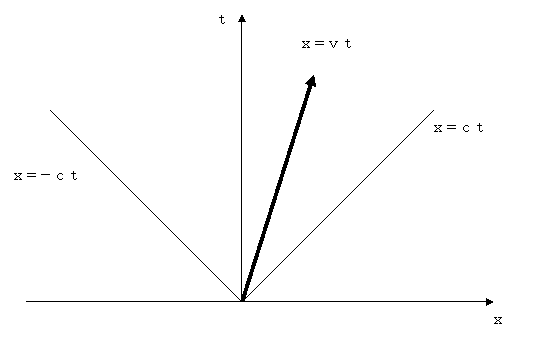
(2)Klein-Gordon方程式における実際の電子の動き
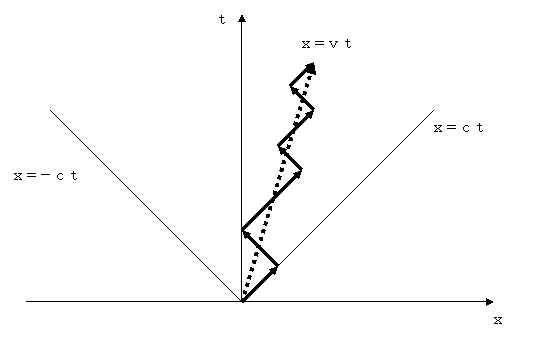
矢印の傾きが常に![]() であることに注視してください。
であることに注視してください。
「①式は何を表しているのでしょうか?」という問題に戻りましょう。
実は、①式は、次のようなことを表しています。
電子は、期間![]() の間に平均
の間に平均![]() 回、なにかに跳ね返されて、折り返します。右に進んでいたものが方向を変えて左に進むという、方向を変える回数が、平均
回、なにかに跳ね返されて、折り返します。右に進んでいたものが方向を変えて左に進むという、方向を変える回数が、平均![]() 回ということなのです。
回ということなのです。
そして、折り返してから、次にまた折り返すまでに進む、距離に相当するものが、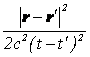 であるということです。
であるということです。
私達を構成している電子は、本来光の速さで進めるのに、何かに跳ね返されて、行きつ戻りつをしてしまいます。その結果、電子は光のようにはなれずに、結果として遅い速度でしか動けないのです。
私たちは本来、光のように自由であったのに、何かがきっかけで、のろまなものになってしまったのかもしれませんね。