2007/8/11 二重スリットの実験の真相
経路積分とフラウンホーファー回折
①スリットの幅が広い場合:Pに到達する波は位相がそろっているが、Qはそろっていない。
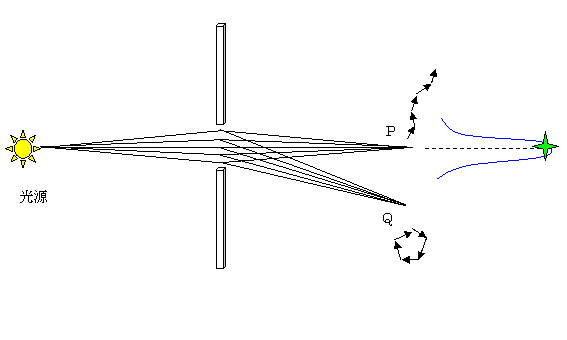
②スリットの幅が狭い場合:Qに到達する波は位相を完全に打ち消しあうほど十分な量ではない。
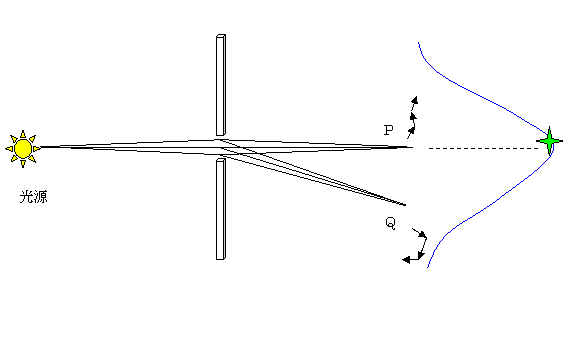
スリットがゆらぐと、Pの位相がそろわなくなり、Qの位相がそろってくる。
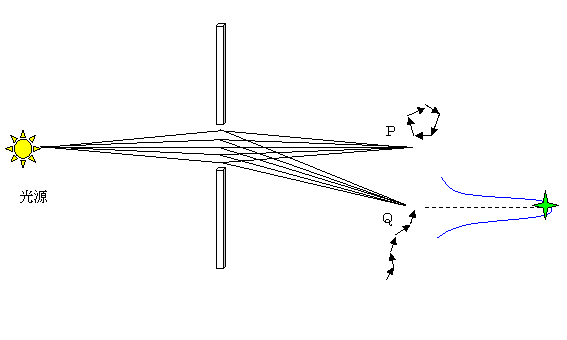
①スリットの幅が広い場合の例
②スリットの幅が狭い場合の例
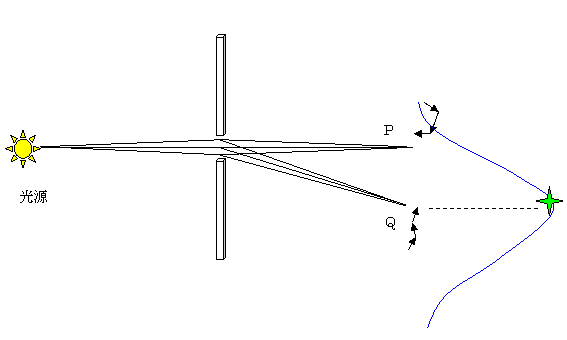
経路積分と干渉
山は位相がそろい、谷は位相がそろわない。
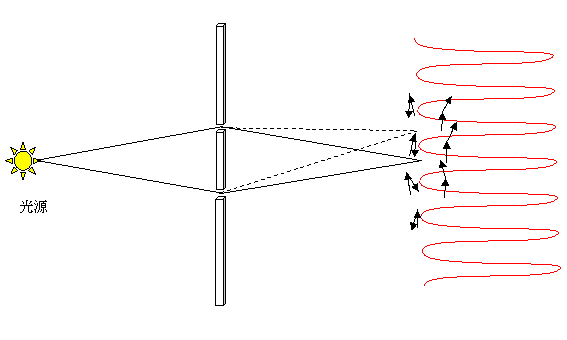
干渉と回折を合わせると、それぞれの図の積のイメージになる。
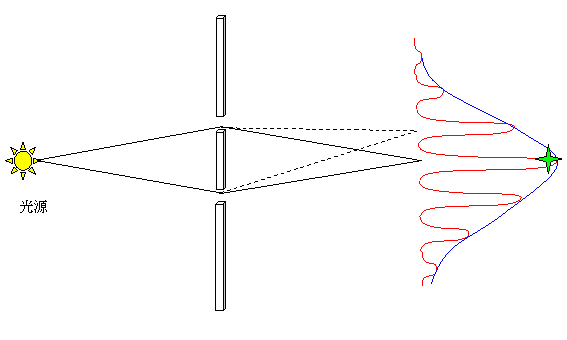
スリットがゆらぐと、位相がそろう位置つまり山の位置がゆらぐ。
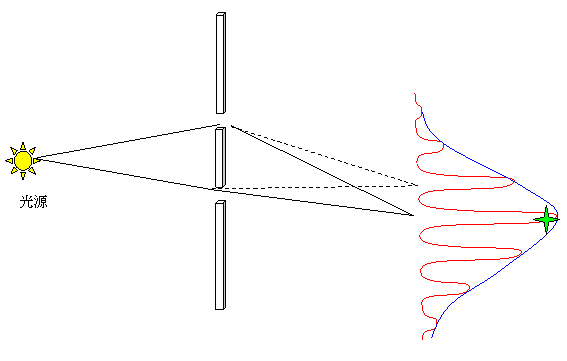
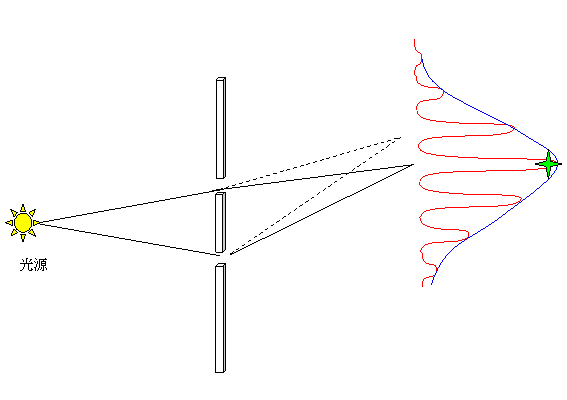
重ね焼あるいは時間平均をすると、再び干渉縞が見えてくる。
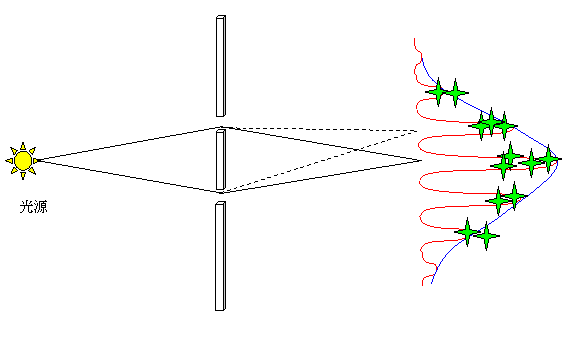
○光源は、光でも電子でも良い。
○二重スリットの実験は、波の「干渉」と「回折」そして「ゆらぎ」で説明できる。
○確率や、粒子というモデルを持ち出す必要はない。
○日立基礎研究所の外村彰氏らの電子による二重スリットの実験に関する論文、
(「Demonstration of single-electron buildup of an interference pattern」
A.Tonomura,J.Endo,T.Matsuda,T.Kawasaki,and H.Ezawa[ American Journal of Physics 57, 117-120 (1989)])を読むと、ゆらいでいるのはバイプリズムのポテンシャル。
つまりスリットがゆらいでいる。
光源からスリットに到達した波動関数
![]()
スリットからスクリーンに到達した波動関数
![]()
従って、経路積分の考え方を使うと、光源からスクリーンに到達した波動関数は、それぞれの積をスリットの幅で足し合わせたものになる。
![]()
![]()
ポテンシャル![]() がゆらぐと波動関数の位相がゆらぎ、結果干渉した後の波の山や谷の位置がゆらぐ。
がゆらぐと波動関数の位相がゆらぎ、結果干渉した後の波の山や谷の位置がゆらぐ。
○実験では、ぎりぎりの感度で撮像しているため、山頂のごく狭い領域(所謂、エアリーディスクの中心部)のみが映ることになる。これが、スクリーン上でアットランダムに観測される輝点である。
![]()
ファインマンさんの言葉。
○(位相を表わす矢印を足しあわすという経路積分の基本則を述べた後・・・)この基本則さえ念頭においていれば、学生はたとえ「波束の収縮」などというものにでくわしても、まごつかないですむはずである。(「光と物質のふしぎな理論-私の量子電磁力学」(R.P.ファインマン著/岩波書店) p102)
○実は電子とは、僕たちが使っている仮説なのだ。これが自然のしくみを理解するうえで、ほとんど実在していると言えるくらい便利だということだ。(「ご冗談でしょう、ファインマンさん(上)」(R.P.ファインマン著/岩波現代文庫) p107)