2007/8/11�@������b�������̓�d�X���b�g�̎����͔g�����Ő����ł���
������b�������̓�d�X���b�g�̎����́u�Ȋw�j��ł������������v�ƌ����Ă��܂��B
����́A���̓d�q���g������d�X���b�g�̎�����g��������������Ă݂܂��B
���̋c�_�́A���̃z�[���y�[�W�������ɂȂ��Ă�������l�X�Ȃ��������Ă���
�~������Y��
�D���N�G��
�����ǍF��
�֓��ێ�
�������
������v��
�Ƃ̃��[���ł̂��Ƃ�����Ƃɍ쐬����Ă��܂��B
���ɔ~������Y������́A���̓�d�X���b�g�̎����̃����_���Ɋϑ������P�_���ǂ̂悤�ɂ��Č���邩�̏d�v�Ȃ��������܂����B
�y�P�z��炬���l�����邱�Ƃɂ��A�g���������d�X���b�g�̎������������B
�������Ɏ擾���Ă����������A��d�X���b�g�̎����Ɋւ��������b�������̊O�������̘_���i�uDemonstration of single-electron buildup of an interference pattern�vA.Tonomura,J.Endo,T.Matsuda,T.Kawasaki,and H.Ezawa[ American Journal of Physics 57, 117-120 (1989)]�j��ǂ�ł݂܂����B
�~�������w�E�̂悤�ɁA���̎����ł͎��́A�u��炬�v���d�v�ȃJ�M���ɂ����Ă��܂��B�u��炬�v���l���ɓ���邱�Ƃɂ���āA���q�Ƃ��Ă̓d�q�������o���Ȃ��Ă��A�g������������A���̎����̌��ʂ�����ł��邱�Ƃ�������܂����B
�u��炬�v�̒��ŁA���̎����ɍł��e����^���Ă���̂́A�o�C�v���Y���̒����ɂ���t�B�������g�ł��B
�t�B�������g�����|�e���V�����G�l���M�[����炢�ł��܂��B
�O���_���́i�P�j��
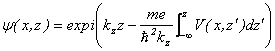
�̒���![]() ���A�t�B�������g�����|�e���V������\���Ă��܂����A����
���A�t�B�������g�����|�e���V������\���Ă��܂����A����![]() �͎��́A
�͎��́A![]() ��
��![]() �����̊��ł͂Ȃ�����
�����̊��ł͂Ȃ�����![]() �̊��ɂ��Ȃ��Ă���͂��ł��B�܂莞�ԂƋ��ɂ�炢�ł���͂��ł��B����ɂ��̂�炬�͌�ōl�@����悤�Ƀu���E���^���I�ł��̂ō��E�Ώ̂ł͂Ȃ��͂��ł��B
�̊��ɂ��Ȃ��Ă���͂��ł��B�܂莞�ԂƋ��ɂ�炢�ł���͂��ł��B����ɂ��̂�炬�͌�ōl�@����悤�Ƀu���E���^���I�ł��̂ō��E�Ώ̂ł͂Ȃ��͂��ł��B
���̃|�e���V��������炢�ł��邽�߁A�O���_���́i�Q�j��
![]()
��![]() �̓o�C�v���Y������o�Ă����g���ƂɈقȂ����l�ɂȂ�͂��ł��B�o�C�v���Y���ɂ͎����玟�ւƓd�q�g�������Ă䂫�A���̔g���o�C�v���Y���̏o���ɓ��B����܂łɎ�e���̏W�ς�
�̓o�C�v���Y������o�Ă����g���ƂɈقȂ����l�ɂȂ�͂��ł��B�o�C�v���Y���ɂ͎����玟�ւƓd�q�g�������Ă䂫�A���̔g���o�C�v���Y���̏o���ɓ��B����܂łɎ�e���̏W�ς�![]() �����܂�Ɓi�Q�j���͓ǂ߂܂��B�|�e���V��������炢�ł��邽�߁A���g���o�C�v���Y���̒��Ŏ��e���ƁA���g�����e���Ƃł́A��ʂɈقȂ�܂��B����ŁA�g�ɂ����
�����܂�Ɓi�Q�j���͓ǂ߂܂��B�|�e���V��������炢�ł��邽�߁A���g���o�C�v���Y���̒��Ŏ��e���ƁA���g�����e���Ƃł́A��ʂɈقȂ�܂��B����ŁA�g�ɂ����![]() �̒l���قȂ邱�ƂɂȂ�̂ł��B
�̒l���قȂ邱�ƂɂȂ�̂ł��B
�O���_���́i�S�j��
![]()
�����Ȃ�\�����ł����A������![]() �������Ă��܂�����A���ꂾ�Ɗ��Ȃł��玞�ԂƋ��ɂ�炬�܂��B
�������Ă��܂�����A���ꂾ�Ɗ��Ȃł��玞�ԂƋ��ɂ�炬�܂��B
������g������A�ł��B
�O���_���́i�R�j��
![]()
�����E����X�N���[����ɓ��B����g���ł����A�����ɂ�![]() �������Ă��܂�����A�o�C�v���Y������X�N���[���Ɏ��镔���̔g���̓t�B�������g�̂�炬�̉e�����āA�ʑ�����炢�ł��܂��܂��B
�������Ă��܂�����A�o�C�v���Y������X�N���[���Ɏ��镔���̔g���̓t�B�������g�̂�炬�̉e�����āA�ʑ�����炢�ł��܂��܂��B
�g��![]() ����炢�ł��܂��Ƃ��̊��̗l�q���ȉ��Ɍ��Ă݂܂��傤�B
����炢�ł��܂��Ƃ��̊��̗l�q���ȉ��Ɍ��Ă݂܂��傤�B
�O���_���́i�R�j���ɂ��A�����炭��g�̔g���x�N�g���́A![]() �ł��B
�ł��B
�܂��E���炭��g�̔g���x�N�g���́A![]() �ł��B
�ł��B
�������A�������̏ꍇ�́A��炬���l���ɓ���܂��̂ŁA�������![]() �ƉE�����
�ƉE�����![]() �͈�ʂɓ���������܂���B����́A�|�e���V����
�͈�ʂɓ���������܂���B����́A�|�e���V����![]() �����E�Ώ̂ɂ�炪�Ȃ����ƂɋN�����܂��B�����ŁA
�����E�Ώ̂ɂ�炪�Ȃ����ƂɋN�����܂��B�����ŁA
�����炭��g�̔g���x�N�g����![]() �ƁA�E���炭��g�̔g���x�N�g����
�ƁA�E���炭��g�̔g���x�N�g����![]() �Ƃ��ꂼ�ꏑ���Ă݂܂��B�i
�Ƃ��ꂼ�ꏑ���Ă݂܂��B�i![]() ���邢��
���邢��![]() �ɂ��Č��Ă݂Ă��A���g�A���g�A��O�g����ŁA�قȂ�l�ɂȂ�܂��B�j
�ɂ��Č��Ă݂Ă��A���g�A���g�A��O�g����ŁA�قȂ�l�ɂȂ�܂��B�j
�}�P�D�����炭��g��![]() �ƉE���炭��g��
�ƉE���炭��g��![]() ���������ꍇ
���������ꍇ
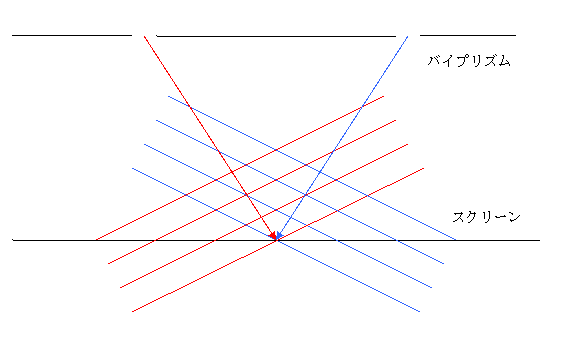
�P�_�́A�X�N���[���̒����Ɍ���܂��B
�}�Q�D�����炭��g��![]() ���E���炭��g��
���E���炭��g��![]() �̕����傫���ꍇ
�̕����傫���ꍇ
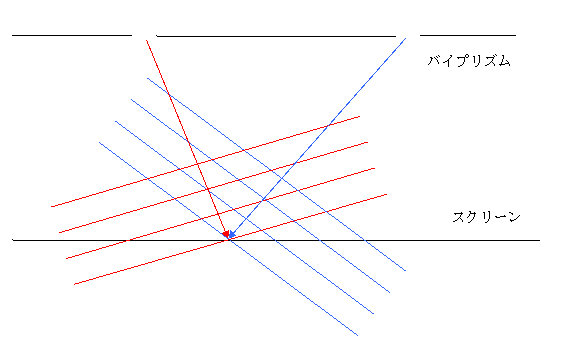
�P�_�́A�����ɂ���܂��B
�}�R�D�����炭��g��![]() ���E���炭��g��
���E���炭��g��![]() �̕����������ꍇ
�̕����������ꍇ
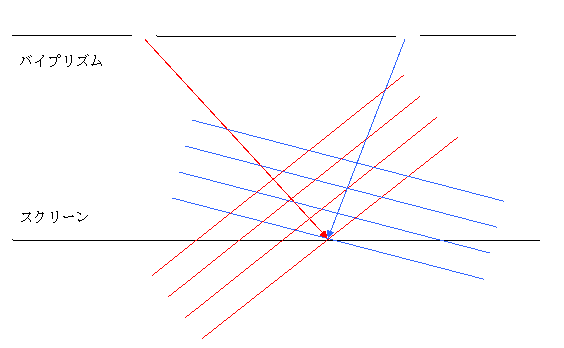
�P�_�́A�E���ɂ���܂��B
���ꂪ�A�����_���Ȉʒu�Ŋϑ�������d�g�݂ł��B
�t�B�������g�����|�e���V��������炢�ł��邽�߁A���̃v���Y����ʂ��Ă���g�̔g��![]() �ƉE�̃v���Y����ʂ��Ă���g�̔g��
�ƉE�̃v���Y����ʂ��Ă���g�̔g��![]() �́A��炬�̉e���ő傫���Ȃ����菬�����Ȃ����肵�܂��B���̌��ʁA��}�̂悤�ɓ�̔g�����߂����ʒu�����̎��X�ɂ���āA�قȂ�킯�ł��B
�́A��炬�̉e���ő傫���Ȃ����菬�����Ȃ����肵�܂��B���̌��ʁA��}�̂悤�ɓ�̔g�����߂����ʒu�����̎��X�ɂ���āA�قȂ�킯�ł��B
���݂̗ʎq�_�ł́A�}�P�̏ꍇ�����l���Ă��炸�A�ȉ��̐}�Ŋۂ������Ƃ��낪���Ȃ̈ʒu�Ƃ����Ă���킯�ł�����A�������̉��߂Ƃ͍��{�I�ɈقȂ�܂��B
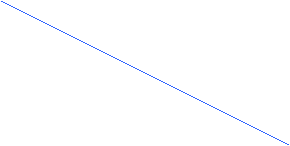
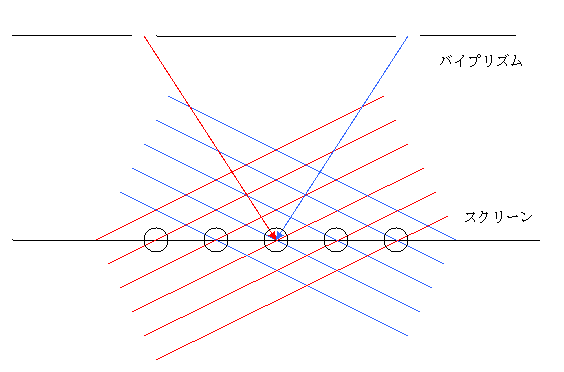
���݂̗ʎq�_�͔��ɐÓI�ȃC���[�W�ł����A��炬���l�������������̏ꍇ�́A��������{�̃T�[�`���C�g���Ɨ����Ė��Ɍ��̔g��U��T���Ă���悤�ɁA�ƂĂ����I�ȃC���[�W�ɂȂ�܂��B
���ɁA�d�q�g���キ���Ă������Ƃ��ɁA�����ł͉��́A�P�_�Ƃ��Ċϑ������̂����l���čs���܂��傤�B
���ۂ̎����ł́A�o�C�v���Y���̊J�������f���^���̂悤�ȗ��z�I�Ȃ��̂ł͂Ȃ��A�L���̑傫���������Ă��邽�߁A��L�̊����ʂɂ���ɉ�܌��ʂ������܂��B
�����A�t���E���z�[�t�@�[��܂ł��B
���̂��߁A�X�N���[����̓d�q�g�̋��x�́A![]() ���ŕ\����銱�Ȃ�
���ŕ\����銱�Ȃ�![]() ���i
���i![]() �j�ōi�荞�`�ɂȂ�܂��i���}�Q�ƁB���l�̈ꕔ�͊O���_����蔲���j�B
�j�ōi�荞�`�ɂȂ�܂��i���}�Q�ƁB���l�̈ꕔ�͊O���_����蔲���j�B

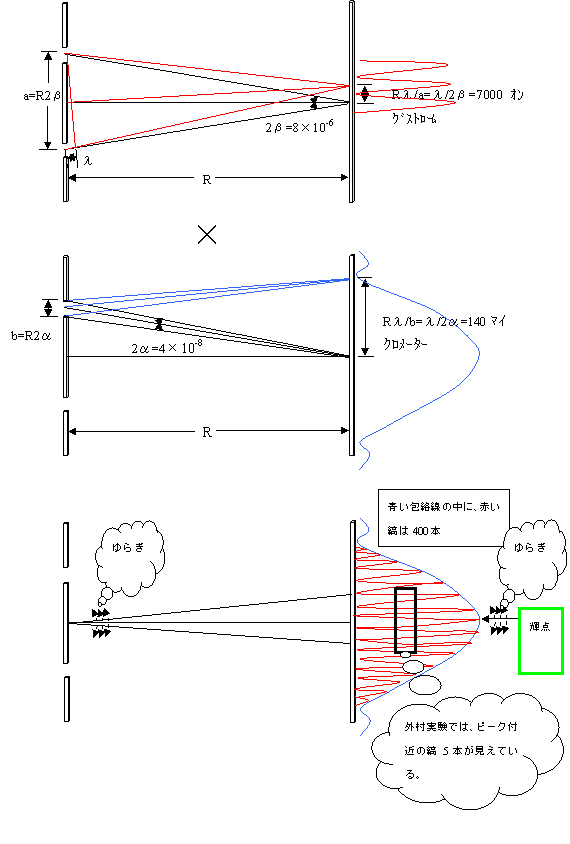
�X�N���[����̓d�q�g�̋��x�́A�R���X���C�X�������̊����ɂȂ�܂��B�O�������ł�400�X���C�X�ł��B
����Ɏ����ł́A���肬��̊��x�ŎB�����Ă��邽�߁A�R���̂��������̈�i�����A�G�A���[�f�B�X�N�̒��S���j�݂̂��f�邱�ƂɂȂ�܂��B���ꂪ�A�X�N���[����Ŋϑ������P�_�ł����Ǝ��͎v���܂��B
�����Ă��̎R�����O�q�̂�炬�ɂ���āA�ӂ�ӂ�Ƃ���̂��Ǝv���܂��B
�ꂪ��炬�A�d�q�g����炮���߁A�t���E���z�[�t�@�[��܂̕��z�̃s�[�N�������_���Ɍ����̂ł��B�����āA�d�q�e������o�����d�q�g���ア���߁A�s�[�N�̕������������e�����킯�ł��B
�ǂ��ł��傤���B�����ɂ��A�d�q�Ɍ����܂��B
�X�N���[����Ń����_���Ɋϑ������P�_�́A�����܂ł��g�ł���܂��āA�d�q�ȂǂƂ������q�����݂���̂ł͂Ȃ��Ǝv���܂��B
�ȏ�̋c�_����������A�������́u�f���q�ȂǂƂ������̂͑��݂��Ȃ��v�ƌ�����������������܂���B
���ȏ�̋c�_�́A�ʎq�_�̏펯�ɂȂ����R�y���n�[�Q�����߁i�����A�g�����̊m�����߁j�ɐ^��������t������V�������߂ł��B�����ė��q�ƌ����T�O��ے肷����̂ł��B
�y�Q�z�o�C�v���Y���̃t�B�������g�����|�e���V��������炢�ł��鍪��
�t�B�������g�����|�e���V����![]() ����炢�ł���Ƃ��������͈ȉ��̂Ƃ���ł��B
����炢�ł���Ƃ��������͈ȉ��̂Ƃ���ł��B
�O���_���́i�Q�j���Ɓi�R�j���̊Ԃ̕��͂̒���
![]() �A
�A![]()
�Ƃ������������܂��̂ŁA![]() ����������A
����������A
![]()
�ƂȂ�܂��B
���̎����O���_���́i�P�j���ɑ������A
![]()
�ƂȂ�܂��āA�w�����̓ڂ́A���̃z�[���y�[�W
�u�o�H�ϕ��Ɍ���g�����Ɨ��q���̓�d���A�����Ă�荪���I�ȑ��݁v�̒��̇C���̉��ɂ���A
![]()
�ɂقڈ�v���܂��B
���̃z�[���y�[�W�̒��ŁA���͂��̏��![]() �Ɩ��Â�
�Ɩ��Â�
![]()
�ŕ\�������̂������_���ȏ�ɂȂ�Ǝw�E���Ă��܂��i�G���̌܍s�゠����ł��B�j�B
�����ĕ����̕��X�Ƙb���Ƃ��͒p���������̂ł������͂�����،��\���ƌĂ�ł��܂��B
�V�����f�B���K�[�������̉��ł���![]() �́A���̃����_���ȏ�
�́A���̃����_���ȏ�![]() �̕��ρi���Ғl�j���Ƃ������̂ł��B
�̕��ρi���Ғl�j���Ƃ������̂ł��B
�ȂɂŊ��Ғl���Ƃ邩�Ɛ\���܂��ƁA�Θ_�I�ȏꍇ�A���̊��Ғl�͐��K���z���łƂ��܂��B�i���K���z���Ƃ́A�����_���E�H�[�N�i�u���E���^���j�̉��ɑ��₵�����̂ł��B�j
�܂�![]() �̂�炬�́A�Θ_�I�ȏꍇ�̓u���E���^���Ń��f�����ł���Ƃ����킯�ł��B
�̂�炬�́A�Θ_�I�ȏꍇ�̓u���E���^���Ń��f�����ł���Ƃ����킯�ł��B
����ȕ���![]() �͂�炢�ł���̂ł��B�����ă|�e���V����
�͂�炢�ł���̂ł��B�����ă|�e���V����![]() ����炢�ł���̂ł��B
����炢�ł���̂ł��B
�O���_���ł́A�^���G�l���M�[
![]()
���Ȃ����������Ă��܂��̂ŁA�{���V�����f�B���K�[�������̔g�����́A
![]()
�Ə�����܂��B
���̂Ȃ��́A
![]()
�̕��������邱�Ƃɂ���āA�����_���ɂ�炢�ł����![]() �ɑ��āA���ω����鑀�삪����܂��B
�ɑ��āA���ω����鑀�삪����܂��B
���ꂪ�A�u�V�����f�B���K�[�������̉��ł���![]() �́A�����_���ȏ�
�́A�����_���ȏ�![]() �̕��ρi���Ғl�j���Ƃ������́v�̈Ӗ�����Ƃ���ł��B
�̕��ρi���Ғl�j���Ƃ������́v�̈Ӗ�����Ƃ���ł��B
�܂�A�V�����f�B���K�[�������̉��ł���g����![]() �͋ߎ��I�Ȃ��̂ɂ����Ȃ��̂ł��B
�͋ߎ��I�Ȃ��̂ɂ����Ȃ��̂ł��B
�f�r�b�h�E�{�[���̌��t�����p���Ă����܂��傤�B
�u��̂�炬�̓����_���ň�肵�Ă��Ȃ��B�ʎq�_�ŗp������ ��̒l�́A���鎞�Ԃɂ킽���Ă̎��ԓI���ςł���B��̂�炬�́A�ʎq�͊w���ΏۂƂ��Ă��郌�x���������Ɖ��ʂ̃��x���ɋN��������̂ł���B����́A�����ȉt�H�̃u���E���^������艺�ʂ̃��x���ł��錴�q���x���ɋN������̂Ƃ��傤�Ǔ����ł���B�����Ă܂��j���[�g���̉^���@�����t�H�̕��ϓI�ȐU�������K�肵�Ă���悤�ɁA�V�����f�B���K�[�̔g����������
��̕��ϓI�ȐU�������K�肵�Ă���̂ł���B�v�i�S�̐��Ɠ�������p150�j
�y�R�z�Ȃ��^���G�l���M�[�����ϑ�������邱�ƂɂȂ�̂�
�^���G�l���M�[�ɑ�������
![]()
�̕������������ό`���܂��ƁA���K���z���ɂȂ邩��ł��B�i����́A�u�t�@�C���}���o�H�ϕ��Ɨʎq�͊w�v�iR.P.�t�@�C���}���^A.R.�q�b�u�X���@�}�O���E�q���j��A�u�ʎq�͊w�ƌo�H�ϕ��v�iR.P.�t�@�C���}���^A.R.�q�b�u�X���@�݂������[�j�Ȃǂ̒��Ńt�@�C���}�����悭����@�ł��B�j
�݂ɂ����ł����A���̃z�[���y�[�W�u�o�H�ϕ��Ɍ���g�����Ɨ��q���̓�d���A�����Ă�荪���I�ȑ��݁v�̒��̇C��
![]()
�������\���Ă��܂��B
����ƁA���K���z��
![]()
�Ƃ��r���Ă݂܂��ƁA
![]()
�Ƃ����āA���Ԃ������ɂ���A�҂������v���܂��B
�^���G�l���M�[�����ԂŐϕ��������̂��w�����̏�ɍڂ��āA����Ɏ��Ԃ������ɂ���ƁA���̎w�������Ȃ�Ɛ��K���z���ɂȂ��Ă��܂��I�Ƃ����̂��A�t�@�C���}���̌o�H�ϕ��̖����ȂƂ���Ȃ̂ł��I�B
�t�@�C���}���̌o�H�ϕ��������܂��ƁA�V�����f�B���K�[�������̉�![]() �́A
�́A
![]()
�ƈ�ʓI�ɉ����Ă��܂��܂��I�B![]() �͊��Ғl���Ƃ�Ƃ����Ӗ��ł��B
�͊��Ғl���Ƃ�Ƃ����Ӗ��ł��B
���Ғl���Ƃ�Ȃ���Ȃ�Ȃ��̂́A�|�e���V�����G�l���M�[����炢�ł��܂��Ă��邩��ł��B
������t�@�C���}��-�J�b�c�̌����ƌĂт܂��B
���Ԃ������ɂ��邱�Ƃ̓��[�N���b�h���Ɛ\���܂��āA�z�[�L���O���r�b�O�o�����_�ʼnF���̏��߂̎��Ԃ������ɂ����Ƃ������ƂŗL���ł��B
�z�[�L���O�͏d�͏�Ƀt�@�C���}���̌o�H�ϕ����_�ɂ��K�p�����̂ł��B