���ʂƂ������̂�z�肷���T
���͗��Ȃ̂��g�Ȃ̂��A�d�q�͗��Ȃ̂��g�Ȃ̂��A�j���[�g���A�z�C�w���X�A�A�C���V���^�C���A�h�u���C�ȂǑ����̕����w�ҒB�ɂ���ċc�_����Ă������Ƃł��B���݂ł͌���d�q�͗��ł�����g�ł�����Ƃ���Ă��܂��B�V�����f�B���K�[�������ŕ\�������g�����ł���A���A�l���\���̊m���͊w�ŕ\�������u���E���^�����闱�q�ł���Ƃ���Ă��܂��B������{�[�A����������ł��B
�u�o�H�ϕ��Ɍ���g�����Ɨ��q���̓�d���A�����Ă�荪���I�ȑ��݁v�̒��ł��A��d�X���b�g�̎����ɂ�����g�����Ɨ��q���̓�d���͑�������T�O�ł͂Ȃ��Ƃ������b�����܂����B�X�N���[����Ŋϑ������A�b�g�����_���ȋP�_�̓u���E���^������ʎq�͊w�I���q��\�����̂ł���Ƃ������b�����܂����B
����A�u�܂������ƍX�V�����v�̒��ł́A���̐��͔g�����Ő����ł���Ǝ��͌����Ă��܂��B�f���q�Ȃǂ͔ے肷��Ƃ������Ă��܂��B
���q�͑��݂���̂ł��傤���A���݂��Ȃ��̂ł��傤���H
����́A�ꌩ���q�̑��݂𗠕t����悤�Ɍ�����u���E���^�����g���āA�t�ɗ��q����ے肵�Ă݂܂��B����ɗ��q�╨���̍ł��T�^�I�ȓ����ł��鎿�ʂ̊T�O��ے肵�܂��B
�j���[�g���͊w�ȗ��A![]() �Ə����Ε����w�ł͎��ʂ�\�����̂Ƃ����̂��펯�ł����B����̍l�@�ł́A���܂�
�Ə����Ε����w�ł͎��ʂ�\�����̂Ƃ����̂��펯�ł����B����̍l�@�ł́A���܂�![]() �Ə����Ă������̂��A���ʂł͂Ȃ����͕ʂ̊T�O��\�����̂ł��邱�Ƃ�������������܂��B
�Ə����Ă������̂��A���ʂł͂Ȃ����͕ʂ̊T�O��\�����̂ł��邱�Ƃ�������������܂��B
����̍l�@��ǂݏI����āA�������e���[���ł���A���Ȃ��͎������g���f���q�Ȃǂ���o���Ă���u���v�ł͂Ȃ����Ƃ� �D�ɗ�����ł��傤�B�u���v�ł͂Ȃ������Ȃ�ċ����čl�����Ȃ��Ƃ������́A����ȏ�ǂݐi�܂Ȃ��ŁA���������̃y�[�W����ĉ������B
�ł͎Q��܂��B
�X���C�h�O���X�ɉԕ����̂��A�����ɐ��H�����炵�ăJ�o�[�O���X�����Ԃ��A�������Ŋώ@���܂��B����ƁA�ԕ��̗��q�������݂ŕs�K���ȉ^�������Ă���̂��ώ@����܂��B���̉^�����u���E���^���ł��B
�u���E���^���̓����ɂ́A�ȉ��̂悤�Ȃ��̂�����܂��B
�@�����q�͏����݂Ɉړ��������]�����肷�邪�A���̓����͂���߂ĕs�K���ł���B
�A�s�K���^���͔����q�̎�ށA���x�ɂ͂��Ȃ��B
�B�����q�������Ă���t�̂��S�������قǕs�K���^���͕s�����ɂȂ�B
�C�s�K���^���͌����Ď~�܂�Ȃ��B
�����A�ƇB����A�����q�������Ă���t�̂̂ق��Ƀu���E���^���̌��������邱�Ƃ��킩��܂��B���ہA�����A����A�u���E���^���͔����q�̎�ނɂ��Ȃ��̂Ŕ����q�Ɍ���������Ƃ͍l�����܂���B�����B�̓u���E���^�����t�̂̔S�������ɂ���ĕς�邱�Ƃ������Ă���A���̂��Ƃ���t�̂̂ق��Ɍ���������ƍl������̂ł���܂��B
�u�u���E���^���ɂ��Ĉȉ��̎������藧���Ă���B
![]() �@����D
�@����D
�����ŁA�㎮���ӂ́A�u���E���^�����镨�̂̕��t�ʒu![]() ����̂����2��̕��ςł���(�n��1�����Ƃ���)�B
����̂����2��̕��ςł���(�n��1�����Ƃ���)�B![]() ���C�̒萔�A
���C�̒萔�A![]() ����Ή��x�A
����Ή��x�A![]() ���Փ��x�i�}�����S���ɊW���A�u���E���^�����镨�̂̑��x��
���Փ��x�i�}�����S���ɊW���A�u���E���^�����镨�̂̑��x��![]() �Ƃ���ƁA
�Ƃ���ƁA![]() �͂��̑��x�ɔ�Ⴗ����R���ƂȂ�j�A
�͂��̑��x�ɔ�Ⴗ����R���ƂȂ�j�A![]() �͏\���o�߂������ԁi�Ɍ��Ƃ��ẮA
�͏\���o�߂������ԁi�Ɍ��Ƃ��ẮA![]() �� ���j�ł���B�����āA
�� ���j�ł���B�����āA![]() ���A�{�K�h���萔�ł���B�A�{�K�h���萔�ȊO�́A�ϑ��ɂ���ċ��߂���ʂł���A�t�����X�̕������w���W�����E�y����(J. B. Perrin�A1870 - 1942)���A
���A�{�K�h���萔�ł���B�A�{�K�h���萔�ȊO�́A�ϑ��ɂ���ċ��߂���ʂł���A�t�����X�̕������w���W�����E�y����(J. B. Perrin�A1870 - 1942)���A![]() = 6.5 �~ 1023�i�����ɂ��l���قȂ�j�Ƃ����l�Ă���B�v�i�E�B�L�y�f�B�A�u�u���E���^���v��蔲���j
= 6.5 �~ 1023�i�����ɂ��l���قȂ�j�Ƃ����l�Ă���B�v�i�E�B�L�y�f�B�A�u�u���E���^���v��蔲���j
�����ŁA
![]() �@����E
�@����E
�́A���U�i�{���e�B���e�B�[![]() �̓��j��\���Ă��܂��B�܂�u�g�U���₷���v�ł��B
�̓��j��\���Ă��܂��B�܂�u�g�U���₷���v�ł��B![]() ���}���̔S���ɊW����Փ��x�ł��̂ŁA
���}���̔S���ɊW����Փ��x�ł��̂ŁA![]() ���傫���Ɗg�U���ɂ����A
���傫���Ɗg�U���ɂ����A![]() ���������Ɗg�U���₷���Ȃ邱�Ƃ��킩��܂��B�܂�A�}�����S�������ƃu���E���^���͕s�����ɂȂ�A�t�ɔ}�������炳�炵�Ă���ƃu���E���^���͊����ɂȂ�܂��B
���������Ɗg�U���₷���Ȃ邱�Ƃ��킩��܂��B�܂�A�}�����S�������ƃu���E���^���͕s�����ɂȂ�A�t�ɔ}�������炳�炵�Ă���ƃu���E���^���͊����ɂȂ�܂��B
�E�������������Ă����܂��傤�B
![]()
�ɂ����āA�C�̒萔![]() �̓{���c�}���萔
�̓{���c�}���萔![]() ��p�����
��p�����
![]()
�ł��̂ŁA
![]()
�ƂȂ�܂��B
�܂�A�{���e�B���e�B�[![]() �́A
�́A
![]()
�ƂȂ�܂��B
�u�g��������v�����N�̍����t�˂̌������Ă݂�v��u���ꑊ�ΐ����_�Ɨʎq�����A�����Čo�H�ϕ��v�Ȃǂ̒��ł�����悤�ɁA
![]()
�̊W��p����ƁA
![]() �@����F
�@����F
�ƍŏI�I�ɕ\���܂��B�u���E���^���̓����ł���{���e�B���e�B�[![]() �́A�}���̔S��
�́A�}���̔S��![]() �ɂ���Č��܂�Ƃ����킯�ł��B�i�����q�̐����ɂ͌����Ă��Ȃ��Ƃ������Ƃɒ��ӂ��Ă��������B�j
�ɂ���Č��܂�Ƃ����킯�ł��B�i�����q�̐����ɂ͌����Ă��Ȃ��Ƃ������Ƃɒ��ӂ��Ă��������B�j
���Ă����ŁA�ʎq�_�̘b�ɖ߂�܂��B�u�o�H�ϕ��Ɍ���g�����Ɨ��q���̓�d���A�����Ă�荪���I�ȑ��݁v�̒��ł��b���܂����悤�ɁA�d�q�Ȃǂ̗ʎq�͊w�I���q���u���E���^�������Ă��܂����B����͓�d�X���b�g�̎����ŁA�X�N���[����Ŋώ@�����d�q���A�b�g�����_���Ȉʒu�Ō����邱�Ƃ�����A�d�q�Ȃǂ̗ʎq�͊w�I���q���u���E���^�������Ă��邱�Ƃ��킩��܂��B
�܂�A�d�q�Ȃǂ̗ʎq�͊w�I���q�́A���ɕ��ԉԕ��̂悤�ɂӂ�ӂ�ƃu���E���^�����Ă���̂ł��B
���̃u���E���^���̃{���e�B���e�B�[�́A�u�|�e���V�����G�l���M�[�Ɖ،��\���v��u�o�H�ϕ��Ɍ���g�����Ɨ��q���̓�d���A�����Ă�荪���I�ȑ��݁v�ł��b���܂����悤�ɁA
![]() �@����G
�@����G
�ł����B![]() �͓d�q�ȂǗʎq�͊w�I���q�́u���ʁv�ł��B
�͓d�q�ȂǗʎq�͊w�I���q�́u���ʁv�ł��B
�F���ƇG�����r���Č��܂��ƁA
![]()
�܂�A
![]()
�Ƃ����W���������܂��B
����́A���Ɋ�ȊW���ł��B�����đ傫�Ȗ���������܂��B�܂�A
�u���E���^���̓����ł���g�U���₷����\�킷�{���e�B���e�B�[![]() ���A
���A
�ԕ��̗�ł́A���̔}���ł��鐅�̔S��![]() �ɂ���Ă���̂ɑ��A
�ɂ���Ă���̂ɑ��A
�d�q�̂悤�ȗʎq�͊w�I���q�̏ꍇ�́A�u���E���^�����Ă�������q���̂��̂̎���![]() �ɂ���Ă���ƌ����̂ł���I�H�H�H
�ɂ���Ă���ƌ����̂ł���I�H�H�H
�`���ł��b���܂����悤�ɁA�u���E���^���̌����͔����q�������Ă���t�̂̂ق��ɂ����āA�u�����q�̎�ނɂ��Ȃ��v�ƌ����̂ɁA�ʎq�͊w�I���q�̏ꍇ�͔����q�̂ق��ɂ���ƌ����̂ł���B�d�q�̎��ʂƗz�q�̎��ʁA�N�H�[�N�̎��ʂȂǑf���q�ƌĂ�Ă�����̂̎���![]() �͂��ꂼ��قȂ�܂�����A�ʎq�͊w�I���q�̏ꍇ�̃u���E���^���̌����́u�����q�̎�ނɂ��v�Ƃ������ƂɂȂ��Ă��܂��܂��H�H�H�B
�͂��ꂼ��قȂ�܂�����A�ʎq�͊w�I���q�̏ꍇ�̃u���E���^���̌����́u�����q�̎�ނɂ��v�Ƃ������ƂɂȂ��Ă��܂��܂��H�H�H�B
���̖����͂ǂ����琶�܂ꂽ�̂ł��傤���H
���̖����́A����![]() �̑f���q�ƌ������f����z�肵�����Ƃɂ��܂��B�����āA����
�̑f���q�ƌ������f����z�肵�����Ƃɂ��܂��B�����āA����![]() �̓d�q�ȂǗʎq�͊w�I���q���A���ɕ��ԉԕ��̂悤�ɂӂ�ӂ�ƃu���E���^�����Ă���Ƃ������f����z�肵�����Ƃɂ��܂��B
�̓d�q�ȂǗʎq�͊w�I���q���A���ɕ��ԉԕ��̂悤�ɂӂ�ӂ�ƃu���E���^�����Ă���Ƃ������f����z�肵�����Ƃɂ��܂��B
![]() �ƌĂ����̂́A���͑f���q�̎��ʂȂǂł͂Ȃ��̂ł͂Ȃ��ł��傤���B
�ƌĂ����̂́A���͑f���q�̎��ʂȂǂł͂Ȃ��̂ł͂Ȃ��ł��傤���B
�j���[�g���͊w�ȗ��A![]() �́u���ʁv�ƌĂ�A���q�̓����Ƃ���Ă��܂����B
�́u���ʁv�ƌĂ�A���q�̓����Ƃ���Ă��܂����B
�������A�ʎq�_�̎���ɂȂ��āA���̂悤�Ƀu���E���^���ƐT�d�ɔ�r���Ă݂܂��ƁA![]() �͑f���q�̓����ł͂Ȃ��A�������̔w��ɂ���u�}���v�̓����Ƃ������ƂɂȂ�܂��B
�͑f���q�̓����ł͂Ȃ��A�������̔w��ɂ���u�}���v�̓����Ƃ������ƂɂȂ�܂��B
![]() �́u��̔S���v�Ƃ����悤�Ȃ��̂ɋ߂��Ǝ��͎v���Ă��܂��B
�́u��̔S���v�Ƃ����悤�Ȃ��̂ɋ߂��Ǝ��͎v���Ă��܂��B
�j���[�g���͊w�ȗ��A![]() �́u���ʁv�ƌĂ�Ă��܂������A���ʂƂ����T�O�͌�T�ł���\��������܂��B�܂�A���ʂŋ�ʂ����f���q�Ȃǂƌ������̂��l���邱�Ǝ��́A�Ӗ��̖������Ƃ��Ǝ��͎v���Ă��܂��B
�́u���ʁv�ƌĂ�Ă��܂������A���ʂƂ����T�O�͌�T�ł���\��������܂��B�܂�A���ʂŋ�ʂ����f���q�Ȃǂƌ������̂��l���邱�Ǝ��́A�Ӗ��̖������Ƃ��Ǝ��͎v���Ă��܂��B
�܂�A��d�X���b�g�̎����ŃX�N���[����Ŋϑ������A�b�g�����_���ȋP�_�́A�f���q�Ȃǂł͂Ȃ��̂ł��B
Appendix
�u�o�H�ϕ��Ɍ���g�����Ɨ��q���̓�d���A�����Ă�荪���I�ȑ��݁v�̒��ŁA
�ʎq�͊w�I���q�ł́A
�ʒu���W���A
![]() ����H
����H
���x����Ă��邱�ƁA
�^���ʂ��A
![]() ����I
����I
���x����Ă��邱�ƁA�����Љ�܂����B
�H���ƇI�����A
![]()
�ƂȂ�܂��B�����ό`���Ă݂܂��傤�B
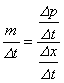
�ɂ����āA
![]() �@�i�j���[�g���̉^���������j�A
�@�i�j���[�g���̉^���������j�A![]() �@�ł��̂ŁA
�@�ł��̂ŁA
![]()
�ł��B
![]()
�Ə����Ă݂�A![]() �͑��x
�͑��x![]() �ɔ�Ⴗ����R���Ɠǂ߂܂��̂ŁA
�ɔ�Ⴗ����R���Ɠǂ߂܂��̂ŁA
![]() �@�́A�Փ��x
�@�́A�Փ��x![]() �Ƃ������ƂɂȂ�܂��i��L�E�B�L�y�f�B�A�̕������Q�Ɓj�B
�Ƃ������ƂɂȂ�܂��i��L�E�B�L�y�f�B�A�̕������Q�Ɓj�B
�܂�
![]() �@���邢�́A
�@���邢�́A![]() �@�ƂȂ�܂��B
�@�ƂȂ�܂��B
���̂��Ƃ�����A![]() ���A�}���̔S����\�킷���̂ł��邱�Ƃ����@����܂��B
���A�}���̔S����\�킷���̂ł��邱�Ƃ����@����܂��B
![]() �͗ʎq�͊w�I���q�ƌĂ�Ă�����̂̎��ʂł͂Ȃ��A���̔w��ɂ����̔S����\���Ă��܂��B
�͗ʎq�͊w�I���q�ƌĂ�Ă�����̂̎��ʂł͂Ȃ��A���̔w��ɂ����̔S����\���Ă��܂��B
�̏d�v�ɏ�����Ƃ��̎������̏d�����Ĉ�̉��Ȃ̂ł��傤���H�H�H