隠れた変数と華厳構造

デビッド・ボームは隠れた変数の理論を提示しました。

今回は、この隠れた変数とは何なのかが解き明かされます。

ファインマンの経路積分では、作用を位相として波動関数は

と記述されますが、デビッド・ボームは位相だけではなく複素数の長さの部分も積極的に波動関数の中に取り入れるべきだとし、

としました。これを最近の確率力学では、

と定義しなおして、

と書きます。このが「隠れた変数」です

一方、量子電気力学における作用は、「ファインマン経路積分と量子力学」（R.P.ファインマン／A.R.ヒッブス著　マグロウヒル）や「量子力学と経路積分」（R.P.ファインマン／A.R.ヒッブス著　みすず書房）のP249の(9-102）式より、

あるいは、

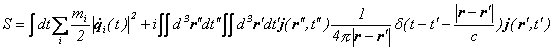
です。

この式を一般的に書きますと、

となります。

二項目が純虚数であることから、

･･･�@

となります。これを隠れた変数の理論の

･･･�A

と比較してみることは興味深いことです。�@と�Aを比べてみますと、

･･･�B

･･･�C

に対応していることがわかります。

�Bで表されるように運動エネルギーが波の位相の役割をしており、隠れた変数とは�Cで表される華厳構造なのです。デビッド・ボームの記述に従えば、

となりますので、

デビッド・ボーム流の隠れた変数は、

ということになります。そしてこれは波動関数の振幅に相当します。

この世を波動で考えてみますと、振幅が華厳構造（そしてこれが隠れた変数）、位相が運動エネルギーで記述できることがわかりました。

前回、「経路積分に見る波動性と粒子性の二重性、そしてより根源的な存在」の中で、波動関数は、

･･･�D

と書け、量子力学的粒子の観点では、ポテンシャルエネルギーの部分を正規分布関数で期待値をとる形になっていることをご紹介しました。

また、「ポテンシャルエネルギーと華厳構造」の中で、

･･･�E

という式をご紹介しましたので、�Dと�Eより、

となりまして、華厳構造を次から次へと正規分布関数（運動エネルギーからきた）で期待値をとってゆく構造になっていることがわかります。

整理しましょう。

この世を波動と考えてみますと、

です。振幅が華厳構造で位相が運動エネルギーです。（そしてこの振幅がデビッド・ボーム流の隠れた変数です。）

この世を粒子と考えますと、

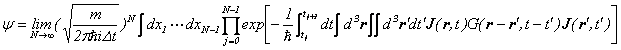
です。華厳構造を運動エネルギーから変形した正規分布関数で期待値をとった形になっています。

波動的な観点と粒子的な観点では、実にシンメトリックな関係になっていることが見てとれます。

この世を波動と考えても、粒子と考えても、華厳構造が重要な役割を果たしていることがわかります。そして華厳構造こそ、デビッド・ボームの隠れた変数である可能性をここに提言しておきます。