�o�H�ϕ��Ɍ���g�����Ɨ��q���̓�d���A�����Ă�荪���I�ȑ���
����̍l�@�ɂ́A���ɏd�v�ȓ��e���܂܂�Ă��܂��B�ʎq�_�ɂ�����g�����Ɨ��q���̓�d���������ĕs�v�c�Ȃ��̂ł͂Ȃ��A���e�����̂ł��邱�Ƃ��ؖ�����܂��B
�܂��V�����f�B���K�[�������̉��ł���g����![]() �́A���͂���ɍ����I�ȏ�
�́A���͂���ɍ����I�ȏ�![]() �̕��ϓI�ȐU�������K�肵�Ă����ɂ����Ȃ����Ƃ��ؖ�����܂��B
�̕��ϓI�ȐU�������K�肵�Ă����ɂ����Ȃ����Ƃ��ؖ�����܂��B
�o�H�ϕ��Ɠ��v���_�i���͂��̓�͕\����́j����g���Ă��܂��̂ŁA�����ł����A�����̂�����́A����ǂ��Ă������Ɠǂ�ł����Ă��������B
�ʎq�_�����������Ă��āA�ʎq�_�����������Ă��Ȃ��̂����͂�����Ƃ킩��܂��B
�o�H�ϕ��̕\���ɂ́A�n�~���g�j�A���o�H�ϕ��ƃ��O�����W���A���o�H�ϕ�������܂��B
����܂ł̂��b�́A���O�����W���A���o�H�ϕ��Řb���Ă��܂����B
�ʒu�Ɖ^���ʂ�Ɨ��ϐ��ƍl���āA�V�����f�B���K�[�������̉��ł���g����![]() ��\�������̂��ȉ��̃n�~���g�j�A���o�H�ϕ��ł��B
��\�������̂��ȉ��̃n�~���g�j�A���o�H�ϕ��ł��B
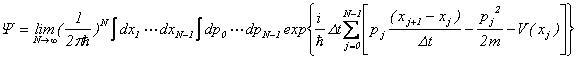 ����@
����@
������L���I��
![]() ����n�~���g�j�A���o�H�ϕ�
����n�~���g�j�A���o�H�ϕ�
�Ə������肵�܂��B�n�~���g�j�A���o�H�ϕ��́A���O�����W���A���o�H�ϕ��ɕό`�ł��܂��B
�@���A
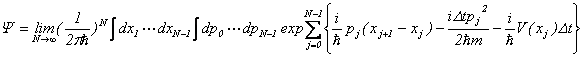
![]()
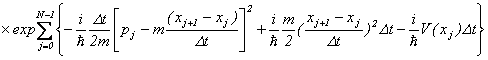 ����A
����A
�ƂȂ�܂����A�^���ʂɊւ���K�E�X�ϕ������s���܂��ƁA
![]()
���A

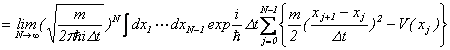 ����B
����B
�ƂȂ�܂��B������L���I��
![]() ������O�����W���A���o�H�ϕ�
������O�����W���A���o�H�ϕ�
�Ə����܂��B
�B���A
![]() ����C
����C
�ƕό`���Ă݂܂��ƁA���O�����W���A���o�H�ϕ��́A���v�͊w�ɂȂ�܂��B�܂�A�|�e���V�����G�l���M�[����
![]()
�̊��Ғl���Ƃ��Ă���`�ɂȂ��Ă��܂��B
![]()
�����K���z��
![]()
�ł��邱�Ƃɒ��ӂ��܂��傤�B�i�^���G�l���M�[�����́A�����z���ɂȂ��Ă��܂��܂����B�j
����Ɠ��l�ɁA�n�~���g�j�A���o�H�ϕ������v�͊w�̌`�ɂ��邱�Ƃ��ł��܂��B
�A���A
![]()
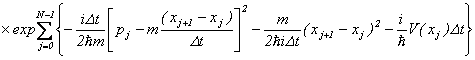
�K�i�����q��ό`���Ă݂�ƁA
![]()
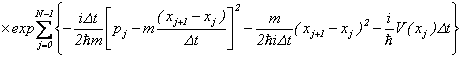 ����D
����D
�ƂȂ�܂��B
![]() ����E
����E
��
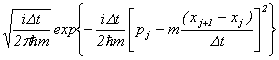 ����F
����F
�����K���z���ɂȂ��Ă��邱�Ƃ��킩��܂��B
�܂�|�e���V�����G�l���M�[�������ʒu���W�Ŋ��Ғl���Ƃ�A����ɉ^���ʂł����Ғl���Ƃ�Ƃ����`�ɂȂ��Ă��܂��B
�����ŁA�g�����Ɨ��q���̓�d���ɂ��čl�@���Ă݂܂��傤�B
�n�~���g�j�A���o�H�ϕ��́A
![]()
�ł������A�ό`���Ă݂܂��ƁA
![]()
�ł��B![]() �͂��Ȃ��݂̕��ʔg�ł��̂ŁA�n�~���g�j�A���o�H�ϕ��ł̕\���͔g�������܂��ɕ\���Ă��܂��B
�͂��Ȃ��݂̕��ʔg�ł��̂ŁA�n�~���g�j�A���o�H�ϕ��ł̕\���͔g�������܂��ɕ\���Ă��܂��B
����A�C��D�̕\���́A�|�e���V�����G�l���M�[�����𐳋K���z���Ŋ��Ғl���Ƃ�`�ɂȂ��Ă��܂��̂ŁA�ʒu���W��
![]()
�Ƃ����m���ߒ��ɏ]���Ă���Ƃ������Ƃ��Ӗ����Ă��܂��B�����ŁA
![]() ����{���e�B���e�B�[�i�W�����j
����{���e�B���e�B�[�i�W�����j
![]() ����u���E���^��
����u���E���^��
![]() ����W�����K�m���ϐ�
����W�����K�m���ϐ�
�ł��B
���̂��Ƃ́A�u���E���^�����Ă���ʎq�͊w�I���q�̑��݂��������Ă��܂��B
�܂藱�q���ł��B
���̗ʎq�͊w�I���q���u���E���^�������Ă��邽�߁A
![]()
�ŕ\�������̂������_���ȏ�ɂȂ�܂��B�C��D����![]() �̕��ρi���Ғl�j����������̂�
�̕��ρi���Ғl�j����������̂�![]() �ł���A���ꂪ���Ȃ킿�V�����f�B���K�[�������̉��ł���g�����ł��邱�Ƃ��Ӗ����Ă��܂��B
�ł���A���ꂪ���Ȃ킿�V�����f�B���K�[�������̉��ł���g�����ł��邱�Ƃ��Ӗ����Ă��܂��B
�o�H�ϕ������낢��Ȍ`�ɕό`���邱�Ƃɂ��A�g�����Ƃ��Ă����߂ł��A���q���Ƃ��Ă����߂ł��邱�Ƃ��킩��܂��B
����̍l�@�ŁA�ʎq�_�̔g�����Ɨ��q���̓�d���́A���e�����̂ł���A�����ĕs�v�c�Ȃ��̂ł͂Ȃ��Ƃ������Ƃ��킩��܂����B
�E���͂�����K�E�X���z�ł��̂ŁA�ʒu���W���A
![]() ����G
����G
���x����Ă��邱�Ƃ��Ӗ����܂��B
�F�����������K�E�X���z�ł��̂ŁA�^���ʂ��A
![]() ����H
����H
���x����Ă��邱�Ƃ��Ӗ����܂��B
�G�ƇH���A
![]()
�ƂȂ�܂��B������s�m�萫�W�ł��B
�Ō�ɁA�،��Ƃ̊W�����Ă݂܂��傤�B
�u�|�e���V�����G�l���M�[�Ɖ،��\���v�̒��ŁA
![]()
�Ƃ��������Љ�܂����B
�C��D�ɂ��ƁA�g����![]() �́A�u���E���^������ʎq�͊w�I���q��
�́A�u���E���^������ʎq�͊w�I���q��
![]() ����I
����I
�̊��Ғl�̌`�ɂȂ��Ă��邱�Ƃ��킩��܂��B�܂�A
![]() �@���邢�́@
�@���邢�́@![]()
�ł��B
�V�����f�B���K�[������
![]()
�́A�u���E���^������ʎq�͊w�I���q��![]() �̊��Ғl�܂蕽�ς��]���������ɂ����Ȃ������̂ł��B
�̊��Ғl�܂蕽�ς��]���������ɂ����Ȃ������̂ł��B
�V�����f�B���K�[�̔g����![]() ���������I�Ȃ��̂Ƃ��āA
���������I�Ȃ��̂Ƃ��āA![]() �̑��݂�����悤�ł��B
�̑��݂�����悤�ł��B
�����Ă���͇I���Ɍ���悤�ɉ،��\���ł��B�i���ꂪ���N�∢���뎯�A���A�A�J�V�b�N���R�[�h���邢�̓z���O���t�B�[�F���ƌĂ����̂�������܂���B�j
�f�r�b�h�E�{�[���̌��t�����p���Ă����܂��傤�B
�u![]() ��̂�炬�̓����_���ň�肵�Ă��Ȃ��B�ʎq�_�ŗp������
��̂�炬�̓����_���ň�肵�Ă��Ȃ��B�ʎq�_�ŗp������![]() ��̒l�́A���鎞��
��̒l�́A���鎞��![]() �ɂ킽���Ă̎��ԓI���ςł���B
�ɂ킽���Ă̎��ԓI���ςł���B![]() ��̂�炬�́A�ʎq�͊w���ΏۂƂ��Ă��郌�x���������Ɖ��ʂ̃��x���ɋN��������̂ł���B����́A�����ȉt�H�̃u���E���^������艺�ʂ̃��x���ł��錴�q���x���ɋN������̂Ƃ��傤�Ǔ����ł���B�����Ă܂��j���[�g���̉^���@�����t�H�̕��ϓI�ȐU�������K�肵�Ă���悤�ɁA�V�����f�B���K�[�̔g����������
��̂�炬�́A�ʎq�͊w���ΏۂƂ��Ă��郌�x���������Ɖ��ʂ̃��x���ɋN��������̂ł���B����́A�����ȉt�H�̃u���E���^������艺�ʂ̃��x���ł��錴�q���x���ɋN������̂Ƃ��傤�Ǔ����ł���B�����Ă܂��j���[�g���̉^���@�����t�H�̕��ϓI�ȐU�������K�肵�Ă���悤�ɁA�V�����f�B���K�[�̔g����������![]() ��̕��ϓI�ȐU�������K�肵�Ă���̂ł���B�v�i�S�̐��Ɠ������� p150�j
��̕��ϓI�ȐU�������K�肵�Ă���̂ł���B�v�i�S�̐��Ɠ������� p150�j
�u���㕨���̂��������v�̒��Łu�j�[���X�E�{�[�A�ɑ�\�����R�y���n�[�Q�����߂��̂ĂāA�f�r�b�h�E�{�[���̃z���O���t�B�b�N�p���_�C�����_���̗p���邱�Ƃɂ���āA���㕨���w�͐����������֖߂邱�Ƃ��o����̂ł͂Ȃ����Ǝ��͍l���Ă���܂��B�v�Ɛ\���܂������A���̍l���͍��ł��ς���Ă���܂���B
�g����![]() �́A�V�����f�B���K�[�������ɏ]���܂��̂ŁA�\���\�ł��B
�́A�V�����f�B���K�[�������ɏ]���܂��̂ŁA�\���\�ł��B
���݂̗ʎq�_�ł́A��Ō��Ă��܂����悤�ɁA�ʎq�͊w�I���q�̓u���E���^���ł����\�L�ł��Ă��܂���̂ŁA���̓����͂܂����������_���ł��B�����āA���̗ʎq�͊w�I���q�̏W���ŋL�q�����ʎq�͊w�I���q��![]() ���܂����������_���ł��B
���܂����������_���ł��B
���̉،��\���ŕ\�����ʎq�͊w�I���q��![]() �̕��ϓI�ȐU�������A�V�����f�B���K�[�������ŋK�肳��Ă���ɂ����Ȃ��̂ł��B�V�����f�B���K�[�������̉��ł���g����
�̕��ϓI�ȐU�������A�V�����f�B���K�[�������ŋK�肳��Ă���ɂ����Ȃ��̂ł��B�V�����f�B���K�[�������̉��ł���g����![]() �́A�����P�ɁA�،��\��
�́A�����P�ɁA�،��\��![]() �̕��ςɂ����Ȃ��̂ł��B
�̕��ςɂ����Ȃ��̂ł��B
���݂̗ʎq�_�ł́A�،��\���ŕ\�����ʎq�͊w�I���q��![]() �̕��ϓI�ȐU�����ł���g����
�̕��ϓI�ȐU�����ł���g����![]() �̎��Ԕ��W�́A�V�����f�B���K�[�������Ő��m�ɗ\�z���邱�Ƃ��ł��܂����A�ʎq�͊w�I���q���Ō�̏u�Ԃɂǂ��Ŋϑ�����邩�́A�܂����������_���Ɍ��܂�Ƃ����������Ƃ��ł��܂���B�����āA���̗ʎq�͊w�I���q�̏W���ŋL�q�����ʎq�͊w�I���q��
�̎��Ԕ��W�́A�V�����f�B���K�[�������Ő��m�ɗ\�z���邱�Ƃ��ł��܂����A�ʎq�͊w�I���q���Ō�̏u�Ԃɂǂ��Ŋϑ�����邩�́A�܂����������_���Ɍ��܂�Ƃ����������Ƃ��ł��܂���B�����āA���̗ʎq�͊w�I���q�̏W���ŋL�q�����ʎq�͊w�I���q��![]() ���܂����������_���ł��B
���܂����������_���ł��B
���݂̗ʎq�_�͂���Ȓi�K�ɂƂǂ܂��Ă��܂��B
�f�r�b�h�E�{�[���́A���̍Ō�̒i�K���܂����������_���ł���ʎq�_�ɖ����ł����A�B�ꂽ�ϐ����_�̕����֍s���܂����B
�A�C���V���^�C���́A���̏̂��Ƃ������āA�u�_�̓T�C�R���V�т��Ȃ���Ȃ��v�Ɨʎq�_������܂����B
�ʎq�_�͊��S�Ȃ̂ł��傤���B
�ʎq�͊w�I���q�́A�{���I�Ƀu���E���^�������Ă���̂ł��傤���B
����Ƃ��A�u���E���^�������闝�R������̂ł��傤���B
�ʎq�͊w�I���q�͉��̃u���E���^�����Ă���̂ł��傤���B
���݂̓u���E���^���ł����L�q�ł��Ă��܂��A���̃u���E���^�����N���������ƂȂ��Ă��鉽�������ɉB��Ă���̂ł��傤���B
�����āA�u���E���^�������Ă���ʎq�͊w�I���q�̏W���ł���،��\���Ƃ̊֘A�́B
�u���E���^�����{���I�ł���A�I�Ȃ��̂ł���A����̍l�@�ŁA�V�����f�B���K�[�������̉��ł���g����![]() ���������I�ȑ��݂����邱�Ƃ͊m���ł��B
���������I�ȑ��݂����邱�Ƃ͊m���ł��B
���ꂪ�،��\���ŕ\�����![]() �ł��B�V�����f�B���K�[�������́A���̉،��\���̕��ϓI�ȐU�������K�肵�Ă���ɂ����Ȃ�����ł��B
�ł��B�V�����f�B���K�[�������́A���̉،��\���̕��ϓI�ȐU�������K�肵�Ă���ɂ����Ȃ�����ł��B
�����Ă��̕��ϓI�ȐU���������߂�ɂ������Ă̊m�����z�́A�Θ_�I�ʎq�_�i�V�����f�B���K�[�������j�̏ꍇ�̓u���E���^���̐��K���z�ł������i�^���G�l���M�[��![]() �Ȃ̂Łj�A���Θ_�I�ʎq�_�̏ꍇ�͂ǂ��Ȃ�̂ł��傤���B
�Ȃ̂Łj�A���Θ_�I�ʎq�_�̏ꍇ�͂ǂ��Ȃ�̂ł��傤���B
����Ȃ�T���̋��������܂���B