Black-Scholes式と華厳構造

金融工学のオプションの価格付け理論で有名なBlack-Scholes式と、量子論の波動関数は大変酷似していることに気付きました。

Fischer BlackとMyron Scholesは、株価の変動率が、ドリフト係数が、拡散係数がの確率過程

に従うと仮定しました。ここでは標準ブラウン運動です。

を用いますと、

となります。従いまして、

となりますが、標準正規確率変数を導入しますと、

となりますので、

となります。ここで、は期待値をとる事を意味します。標準正規分布関数を用いますと、結局

と書けます。における株価は、における株価から、

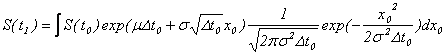
と計算できますし、における株価は、における株価から、

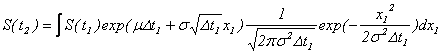
と計算できます。従いまして、における株価は、における初期の株価から、

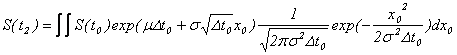
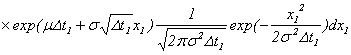
という具合に順番に計算できることになります。式の順番を少し変えてみますと、

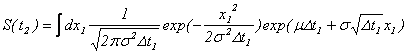
となります。

初期の株価が、によって時間発展し、これの期待値をとったものが、における株価です。

が、によって時間発展し、これの期待値をとったものが、における株価です。

前回、「ポテンシャルエネルギーと華厳構造」の中で、量子論の波動関数が、

で書けることをお話しました。による積分が、

と分割できることから、波動関数は、

と書くことができます。

初期の波動関数、

が、によって時間発展し、これの期待値をとったものが、における波動関数です。

が、によって時間発展し、これの期待値をとったものが、における波動関数です。

･･････

が、によって時間発展し、これの期待値をとったものが、における波動関数です。

株価の場合は、時間発展を決めるものが、つまりドリフト係数とボラティリティーでしたが、

波動関数の場合は、であらわされる、いわゆる華厳構造なのです。

宇宙の隅から隅までそして宇宙開闢からの全ての経歴が畳み込まれたポテンシャルエネルギーによって、波動関数は時間発展します。この波動関数の期待値をとったものが次の瞬間の波動関数です。

そしてその波動関数は、宇宙開闢からそして宇宙全体のあらゆる経験が畳み込まれたポテンシャルエネルギーによって、さらに時間発展してゆくのです。

ある瞬間の私たちの存在は、全宇宙と全時間の相互作用で記述されるこの華厳構造の期待値として記述されます。そしてほんの一瞬あとの事を論じる際にも、やはり全宇宙と全時間の相互作用で記述されるこの華厳構造を考慮しなければならないのです。

一瞬、一瞬の出来事が、全宇宙の存在と全時間の存在と相互依存しているというつくりにこの世界はなっています。

全宇宙と全時間の存在とそれらの相互依存関係を考慮しなければ、次の瞬間のことすら論ずることができないという、驚愕すべき構造にこの宇宙はなっているのです。

私の一秒後は私だけの一秒後では全くないのです。

私の一秒後には、全宇宙の相互依存関係が影響しているのです。

これは、仏教の縁起を数式で表したものと私は考えます。

量子論の波動関数をこのように書き直してみることによって、仏教の縁起の形が手にとるようによく見えるようになったと私は考えています。