�|�e���V�����G�l���M�[�Ɖ،��\��
�ȑO�u�}�b�n�̌����v�̒��ŁA
![]()
�Ƃ����������Љ�܂����B
�E�ӑ�́A�������_�Ԃ̃G�l���M�[�^���ʃe���\���́A�d�͏�̓`�d����ʂ��đ��ݍ�p�����Ă���Ɠǂ߂܂��B
�����Ă���́A�u�t�@�C���}���o�H�ϕ��Ɨʎq�͊w�v�iR.P.�t�@�C���}���^A.R.�q�b�u�X���@�}�O���E�q���j��u�ʎq�͊w�ƌo�H�ϕ��v�iR.P.�t�@�C���}���^A.R.�q�b�u�X���@�݂������[�j��P249��(9-102�j���̍�p
![]()
![]()
���邢�́A
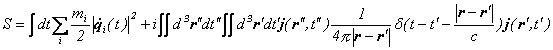
�ɑΉ����܂��B
���̎��͓d����̎��ł����A���̎��ł͂������_�Ԃ̎l���d�����x���d����̓`�d����ʂ��đ��ݍ�p�����Ă���Ƃ������̂ł��B
�����̎�����ʓI�ɏ����܂��ƁA
![]() ����@
����@
�ƂȂ�܂��B
![]()
�|�e���V�����G�l���M�[��![]() �Ƃ��܂��ƁA��p�͈�ʂɁA
�Ƃ��܂��ƁA��p�͈�ʂɁA
![]() ����A
����A
�Ə����܂��B�@�ƇA���ׂ܂��ƁA
![]() ����B
����B
�ƂȂ�܂��̂ŁA�|�e���V�����G�l���M�[�ƌĂ�Ă�����̂��A���͉،��\���ɂȂ��Ă��邱�Ƃ�������܂��B
���Z�̕����ł́A�d�̓|�e���V�����̒��̎��_![]() �̃G�l���M�[�́A
�̃G�l���M�[�́A
![]()
�Ƌ����܂����B�܂��Ód�|�e���V�����̒��̎��_![]() �̃G�l���M�[�́A
�̃G�l���M�[�́A
![]()
�ȂǂƋ����܂������A���̏d�̓|�e���V������Ód�|�e���V�����̋L�q�́A���͑e�G�ȋߎ��������̂ł��B
�{���́A�@���̂悤�ɁA�����鎞��Ԃ̑��ݍ�p����ݍ��،��\���Ń|�e���V�����G�l���M�[�͕\����Ȃ���Ȃ�Ȃ������̂ł��B���̑��ݍ�p�͓`�d����ʂ��ĂȂ���܂��B
�F���J蓂���́A�����ĉF���̋�������܂ł̌o���͂��ׂĂ��̃|�e���V�����G�l���M�[�̒��ɒ~�����Ă���̂ł��I
�ł͎���![]() �ŕ\�����^���G�l���M�[�̈Ӗ����l���Ă݂܂��傤�B
�ŕ\�����^���G�l���M�[�̈Ӗ����l���Ă݂܂��傤�B
�@���ɖ߂�܂��B���x��![]() �ł��̂ŁA�@���́A
�ł��̂ŁA�@���́A
![]()
![]() ����C
����C
�ƂȂ�܂��B
�ʎq�_�ł́A
![]() ����D
����D
�ŕ\�����g�������d�v�Ȗ��������Ă��܂��B
�D�ɇC�������Ă݂܂��ƁA
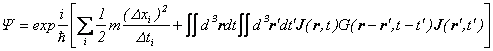
![]()
![]() ����E
����E
����𐳋K���z���i�K�E�X���j�Ɣ�r���Ă݂邱�Ƃ́A���ɋ����[���ł��B
�h���t�g�W����![]() �A�g�U�W����
�A�g�U�W����![]() �̊m���ߒ��́A�W���u���E���^��
�̊m���ߒ��́A�W���u���E���^��![]() ��p�����
��p�����
![]()
�ƕ\�����Ƃ��o���܂��B���̎��̐��K���z���́A
![]()
�Ə����܂��̂ŁA�E�̑�ꍀ
![]()
�Ɣ�ׂĂ݂܂��ƁA����́A�{���e�B���e�B�[��
![]()
�̐��K���z�ł��邱�Ƃ������Ă��܂��B�ʎq�͊w�I���q�ƌĂ����͕̂s�K���ȃu���E���^�������Ă���̂�������܂���B
�܂��{���e�B���e�B�[��![]() �̐��K���z�Ƃ́A
�̐��K���z�Ƃ́A![]() ��
��![]() ���x�ɍL�����Ă��邱�Ƃ��Ӗ����܂��̂ŁA�E�̑�ꍀ�́A
���x�ɍL�����Ă��邱�Ƃ��Ӗ����܂��̂ŁA�E�̑�ꍀ�́A![]() ��
��![]() ���x�L�����Ă��邱�ƂɂȂ�܂��B
���x�L�����Ă��邱�ƂɂȂ�܂��B
�܂�A
![]()
![]()
![]()
�ƂȂ��āA�s�m�萫�W�o���邱�Ƃ��ł��܂��B
�E���́A

�Ə����܂��̂ŁA����́A�،��\���̒��̂ЂƂ̋O���ɒ��ڂ��A���̋O���̂��鎞���ɂ�����![]() �����̊��Ғl���Ƃ邱�Ƃ��Ӗ����Ă��܂��B�����āA�A�����鎞�ԂŎ����玟�ւƊ��Ғl���Ƃ��Ă��������̂��A�g�����ł���Ƃ������ƂɂȂ�܂��B
�����̊��Ғl���Ƃ邱�Ƃ��Ӗ����Ă��܂��B�����āA�A�����鎞�ԂŎ����玟�ւƊ��Ғl���Ƃ��Ă��������̂��A�g�����ł���Ƃ������ƂɂȂ�܂��B
����̓t�@�C���}���|�J�b�c�̌����ƌĂ�Ă��܂��B
�t�@�C���}���̌o�H�ϕ��ɂ����Ď��Ԃ������ɂ��邱�Ƃɂ��A�o�H�ϕ����E�B�[�i�[�ϕ��ŕ\����铝�v�͊w�̐��E�ɕϊ��������Ƃ��Ӗ����Ă��܂��B
����́A�������Ԃł͔g�����������A�������Ԃł̓u���E���^�������闱�q���������Ƃ����߂ł��܂��i���邢�͋������Ԃł͔g�����A�������Ԃł͗��q���j�B
�܂�ʎq�_�ɂ�����A�g�����Ɨ��q���̓�ʐ��i����j�Ƃ́A�������ۂ������Ԃ̕������猩��Ɣg���Ɍ����A�����Ԃ̕������猩��Ɨ��q�Ɍ�����Ƃ������ƂȂ̂ł͂Ȃ��ł��傤���B
�^���G�l���M�[��![]() �ŕ\�����Θ_�I�Ȑ��E�Ƃ́A���̊��Ғl���Ƃ�Ƃ��̕��z�����A���K���z�ł���Ɖ��肷�邱�Ƃɑ�������̂ł��B�����āA���ʂƌĂ�Ă�����̂́A���̐��K���z���̃{���e�B���e�B�[�i�W�����j�ɂЂ��Â��܂��B
�ŕ\�����Θ_�I�Ȑ��E�Ƃ́A���̊��Ғl���Ƃ�Ƃ��̕��z�����A���K���z�ł���Ɖ��肷�邱�Ƃɑ�������̂ł��B�����āA���ʂƌĂ�Ă�����̂́A���̐��K���z���̃{���e�B���e�B�[�i�W�����j�ɂЂ��Â��܂��B
���ʂ��傫���ƕW�����͏������Ȃ��ăV���[�v�ȑ��݂ƂȂ�A�t�Ɏ��ʂ��������Ȃ�ƕW�������傫���Ȃ��Ăڂ₯�����݂ɂȂ�܂��B
�F���̋�������܂ł����āA�F���J蓂���̑S�Ă̌o������ݍ��܂ꂽ�|�e���V�����G�l���M�[�ɂ���āA���݂݂̍�������܂��Ă���Ƃ����\��������͕\���Ă��܂��B
�|�e���V�����G�l���M�[�̒��ɂ�����o������ݍ��܂�Ă��܂��B
�F���J蓂���A�����ĉF���S�̂̂�����o������ݍ��܂ꂽ�|�e���V�����G�l���M�[�̊��Ғl���������̑��݁A�Ƃ������ƂɂȂ�܂��B
�֑��ł����A�����ŁA�،��\�����ŏI�I�ȃy�C�I�t���ƍl���A���Ԃ𖢗����猻�݂ɑk��`���ɏ������߂Ă݂܂��ƁA
![]()
����́A���Z�H�w�̃I�v�V�����̉��i�t�����_�ȂǂɂłĂ���A�u�o�b�N���[�h�C���_�N�V�����v�Ƃ������@�Ɏ��Ă��܂��B
Appendix
�o�H�ϕ��́A
![]()
�ł���܂��̂ŁA�g�����́A
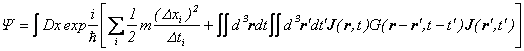
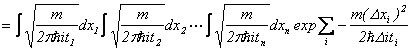
![]()
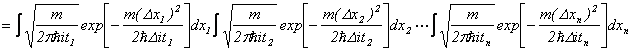
![]()
�Ə����܂��B�،��\���ŕ\�����|�e���V�����G�l���M�[���A�����玟�ւƐ��K���z���Ŋ��Ғl���Ƃ��Ă䂭�`���悭���Ď��܂��B
���m�ȋc�_������Ƃ��̂悤�ɂȂ�܂��B
����͎��̌o�H�ϕ��Ɠ����ł��B
![]()
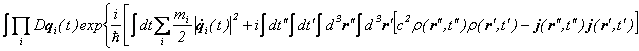
![]()
�����ɁA
![]()
![]()
![]() �ŕ\�����o�H���A���낢��Ƃ��炵�Ă݂����A
�ŕ\�����o�H���A���낢��Ƃ��炵�Ă݂����A
![]()
![]()
�ŋL�q������p![]() ���ɏ��ƂȂ�Ƃ��낪�A�g���d�Ȃ荇���Ĕg�����̐U�����傫���Ȃ�܂��B���̂ق��̌o�H�ɑ�������U���͔g���ł����������ď����Ă��܂��܂��B
���ɏ��ƂȂ�Ƃ��낪�A�g���d�Ȃ荇���Ĕg�����̐U�����傫���Ȃ�܂��B���̂ق��̌o�H�ɑ�������U���͔g���ł����������ď����Ă��܂��܂��B
�g�����̐U�����傫���Ȃ�o�H���A���ۂɌ���錻�ۂł��B