|
|
��T�̓��j���ɁA���X�͕s���ɍs���āA���b��l�ɂ��Ă̍u�����Ă��܂����B
�n�[�o�[�h��w�����̈�������搶�i���́A���莛�ю������t�̒��j�������B���X�͕s�����͖��莛�̕ʉ@�ł���j�̍u���ł��B
�ȉ��́A���̍u������̃����ł��B
��Ƃ����ƁA�j�q���Y���Ɋׂ��Ă��܂������Ȃ̂ŁA�،��ł́A��ƌ��킸�A���N�Ƃ������̂������ł��B
�،��ł́A�܂��W������ɂ���Ƃ������Ƃ����������̂������ł��B
�،��o�̒��̞��Ԍo�ɁA��ߓV�̐��E�ɂ͒�ԁi�����������C���h���l�b�g�j�Ƃ����Ԃ��A�͂�߂��炳��Ă���Ƃ�����Ă��邻���ł��B
�������͂��݂��ɁA�w偂̑��̎��̂悤�Ɍ����Ȃ����Ō���Ă��āA���̌��іڂ͂��ׂĂ��Ƃ炵�Č݂��ɉf�����������̕��łł��Ă���Ƃ����Ă��܂��B
�ЂƂ̕�삪��̂悤�ɖ苿���ƁA����ɉ����邩�̂悤�Ɍ��э�����Ԃ������A��̉������X�Ɩ苿���A�F���̖��Ȃ�����Ȃ�t�ł͂��߂�̂������ł��B
�،��o�̍Ō�̕����Ɂu���@�E�i�i�ɂイ�ق������ق�j�v�Ƃ������̂����邻���ł��B�u���@�E�v�Ƃ́A�@�E�܂肳�Ƃ�̐��E�ɓ��邱�Ƃ��Ӗ����Ă��邻���ł��B�u���@�E�i�v�ł́A�P�����q�i�����ǂ����j�Ƃ������̓������߂�N���o�ꂵ�A55�l�i�������ɂ���Ă�53�l�j���̑����̑P�m���i�P���t�A�P���F�j���K���ċ����������Ă����܂��B
��53�Ԗڂ̑P�m���A���ӕ�F���P�����q�ƌ�荇����ʂł́A�P�����q�͖����̐��҂̋������āA�Ō�ɖ��ӕ�F�̂Ƃ���։��w�������ɁA���ɋ����@�E�ɓ��铹���������܂����B
�P�����q�͌����܂����B
�u�ǂ�����O�ς̖���J���āA���点�Ă��������B�v
���ӕ�F�͂������܂����B
�u�������A��O�ςɓ���Ȃ����B�v
���̎��A���ӕ�F�́A�d�w�Ɛl���w�Ƃ��܂ތ`�����Ēe����܂��ƁA���̉��Ɠ����ɁA�O�ς̖�͎��R�ɊJ���āA�P�����q�́A���łɍ������A��O�ς̒��ɂ��鎩�������o�����̂ł��B
��O�̔����J���ƁA���̒��ɂ͖����̑�O���A���킹���������Ƃ��̂悤�Ɋ�d�ɂ�������̂ł��B�����Ă��̖����̑�O�̒��ɂ́A�܂������̑P�����q���g��������̂ł��B
�P�����q�́A���ӕ�F�̑�O�ςɓ����āA�~�N������}�N���ւ̗l�X�ȊK�w�̉F�������āA�m��̂ł��B
|
|
|
|
|
|

�u�v�ɑ���L�q���A���邢�́A�u�v�̑��݂��A���̊W���̒��ɂ������݂����Ȃ����Ƃ��A�䓛�r�F�͕����v�z��p���ď�}�̂悤�ɏЉ�Ă��܂��B����́A�،��N�w�́u���N�v��}���������̂ł����A�}���́u�`�v�͑��̂a�C�b�C�c�C�E�E�E�E�S�Ă̊W���̒��ɂ̂ݑ��݂��A�u�`�Ƃj�̊W�v�����̑S�Ă̂��̂Ƃ̊W���̒��ɂ̂ݑ��݂��Ă��܂��B
�@�i�u�������G�E�������G�v�w�R�X���X�ƃA���`�R�X���X�x�i�䓛�r�F�j
���̊G���������A�������܂����B
���̊G�͏G��ł��iA�Ƃ͍���̉~�`�����AK�Ƃ͉E���̉~�`�����B���ɂ����Ȃ��ċ��k�ł��B�j�B
���̈��p�́A��}������ɍI����������u�����O�S���w�ƕ����v�i�͍����Y�j����Ƃ������̂ł��B
�u�����O�S���w�ƕ����v�i�͍����Y�j�@���D�P�S�S�|�P�s�ځ`�P�T�s��
�܂��͂��߂ɁA�،��N�w�ɂ����鑶�ݘ_�I�W���Ƃ����l�����Љ�܂��傤�B�`�A�a�A�b�A�c�D�D�D�̌X�̂��͎̂����͂Ȃ��Ƃ��W�͂���܂��B�]���āA�`�Ƃ������̂̑����ɂ͂a�A�b�A�c�D�D�D�Ƃ��ׂĂ̂��̂���������Ă���킯�ł��B�܂�A���ꂼ�ꂪ�݂��ɊW���Ă���A���̑S�̊W�������Ă͉������݂����Ȃ��̂ł��B������䓛���m�́A�}�Q�V�Ɏ����悤�ɁA���܂����o�����Ė��炩�ɂ��Ă��܂��B����́A�����܂ł����u�̐}�ŁA���ԂƋ��ɉ��������A���̊֘A�ɂ���āA���ׂĂ��ς�邱�ƂɂȂ�܂��B
���̂悤�ɍl����ƁA�`�Ƃ������͎̂����������Ȃ��Ƃ��A���̈�̂��̂Ƃ̑��݊֘A�ɂ����Ă`�ł���킯�ł��B�܂�A�`�̓��I�\���̑��̈�̂��̂��B�ꂽ�`�Ŋ܂܂�Ă���A�Ƃ������Ƃ��ł��܂��B�����āA���̂悤�Ȋ֘A���ɂ���āA�`�͂`�ł���A�a�ł��b�ł��Ȃ��A�Ƃ������ƂɂȂ�܂��B�u�ꕨ�̌��N�́A���Ȃ킿�A��ؖ��@�̌��N�B�������̂��̂��A���ꂾ���ŌI�Ɍ��N���邱�Ƃ́A��ɂ��蓾�Ȃ��B��ɂ��ׂĂ̂��̂��A�����ɁA�S�̓I�Ɍ��N����̂ł��B�����̂��̂悤�ȑ��ݎ������A�،��N�w�́w���N�x�Ƃ����܂��B�w���N�x�́w���N�x�ƂȂ��ŁA�،��N�w�̒����I�T�O�ł���܂��v�B
|
|
|
|
|
2006/8/27�@�c�C�X�^�[���_�Ɖ،��o
|
|
****************************
�V���Q���̓��L�L���ŁA�E�F�C�^�[�̎����M�ɗႦ�āu�X�s�m�[���v�̂��b������܂����B����������܂����̂ŐF�X�������܂������ɁA�u�c�B�X�^�[���_��ڂŌ���v�Ƃ����̂������܂����B
http://www.geocities.co.jp/SiliconValley-Oakland/1253/tuistor.html
�����ꂽ�u�}�v�̂ق������ꂢ�ŋC���Ƃ��āA�����̕��͓���Ă����ς����܂���ł������A���̂��ꂪ�F�����ׂĂ̌q�����\���Ă���u�}�v�ɂȂ�̂ł��傤�B
���̐}���̏W�܂肪�A�e�X���q���葶�݂��Ă���،��o�Ɏ�����Ă���Ƃ���̐��E�ɂȂ�̂ł��傤���B
�ǂ̗l�ɃC���[�W����悢�̂ł��傤�B
****************************
�Ƃ�������������������܂����B
�c�C�X�^�[���_�́A�����܂��A�����g�������\���ɋy��ł���܂��A�ȉ��̂悤�Ȃ����������Č��܂����B
****************************
�c�C�X�^�[���_�́A�ʎq�_�Ƒ��Θ_���Ȃ��A�ʎq�d�͏ꗝ�_�̈�Ƃ��Ē��Ђ����_�ƕ���ŗL�]������Ă���悤�ł��B
�X�s�m�[���̃C���[�W�́A�˔��̂˂�A���C���̐��̃C���[�W�ł��B
�����ł��B
������������Ă���d�q�́A���̃��C���̐�1�łł��Ă��܂��B
�����āA���q�́A���C���̐��Q�łł��Ă���̂ł��B
�d�͂̌��Ƃ����d�͎q�́A���C���̐��S�łł��Ă��܂��B
�c�C�X�^�[���_������y�����[�Y�́A���Ԃ��Ԃ����̃��C���̐��łł��Ă���ƍl�����悤�ł��B�����ɓI�ȍ����I�ȑ��݂ł͂Ȃ��A���̎�����A����ɍ����I�ȃX�s�m�[���܂胏�C���̐��łł��Ă���ƍl�����킯�ł��B
�ނɂ��A���Ԃ��Ԃ́A���̃��C���̐��A���邢�͂˂̃l�b�g���[�N�łł��Ă���Ƃ̎��ł��B�m�[�h�ƃ����N�łł��Ă���炵���̂ł��B
�����N�����C���̐���˂̃C���[�W�ł��B
�،��o�̒��̞��Ԍo�ɁA��ߓV�̐��E�ɂ͒�ԁi�����������C���h���l�b�g�j�Ƃ����Ԃ��A�͂�߂��炳��Ă���Ƃ�����Ă��邻���ł��B
�������͂��݂��ɁA�w偂̑��̎��̂悤�Ɍ����Ȃ����Ō���Ă��āA���̌��іڂ͂��ׂĂ��Ƃ炵�Č݂��ɉf�����������̕��łł��Ă���Ƃ����Ă��܂��B
�ЂƂ̕�삪��̂悤�ɖ苿���ƁA����ɉ����邩�̂悤�Ɍ��э�����Ԃ������A��̉������X�Ɩ苿���A�F���̖��Ȃ�����Ȃ�t�ł͂��߂�̂������ł��B
�m�[�h�́A���іڂ̐����̕��ɑΉ����A
�����N�́A�w偂̑��̎��ɑΉ�����悤�Ȋ����ł��B
�A���w偂̑��̎��́A����ɐL�тĂ���̂ł͂Ȃ��A�˔��̂˂̂悤�ɗ�����ɐL�тĂ���킯�ł��B
�����g�͂��̂悤�ȃC���[�W�������Ă��܂��B
****************************
�i���j�X�s�m�[���ɂ��܂��ẮA�u���Θ_�I�d�q��̕������iDirac�������j�v�ƁuDirac�������̓`�d���v�̃y�[�W���Q�ƁB
|
|
|
|
|
|
�u�����u����v�̏�����l�ɁA�����w��13�Ԑ��Ō������Ă����@�B�H�����o�c������c�C�Y�B�O�l�́A��������15�Ԑ��ɓ������u����v�œ����������j�Ɩ�s���}��ԁu���������v�ɏ�荞�ނƂ����������B����������A�����Ƃ��̒j�E���R�́A���łŎ��̂ƂȂ��Ĕ������ꂽ�B
�ꌩ����ӂꂽ��Ɍ��������A�����̃x�e�����Y���E�����d���Y�́A���R�������Ă����ԓ��H���̓`�[���玖���̗��̐^����T�邽�߁A��l�{�������邱�Ƃɂ���B�v
�����m�A���{�����́u�_�Ɛ��v�ł���B
���̉F���ɂ�A�ʂ�B�ʂ����邱�Ƃ��A�ȑO�̓��L�u2006/7/9�@�F���̕\�i�����āj�ʂƗ��ʁv�̒��ł��b���܂������A���̉F���ɂ́A�ǂ����O�Ԗڂ�C�ʂ܂ł���悤�ł��B
A�ʂ́A�悭�����m�̎��������Z��ł��鎞�ԂƋ�Ԃ́u����v�AB�ʂ́A�G�l���M�[�Ɖ^���ʂłł��Ă���u�G�l���M�[�^���ʋ�ԁv�ł��iA�ʂ�B�ʂ̓t�[���G�ϊ��Ō��т��Ă��܂��B�j�B
������C�ʂƂ́A�c�C�X�^�[��Ԃł��B���̃c�C�X�^�[��Ԃ́A��̃X�s�m�[���i�o�X�s�m�[���j�ʂƃɂō\�������c�C�X�^�[���W��=(��,��)�ŋK�肳��܂��B
�������̎���ƁA�c�C�X�^�[��ԂƂɂ́A�ʔ����Ή��W������܂��B
�������̎���ł̌����i�ތ����́A�c�C�X�^�[��Ԃł͓_�ŕ\����܂��B
�t�Ɏ������̎����̓_�́A�c�C�X�^�[��Ԃł͐��ŕ\�����̂ł��B
����̐��̓c�C�X�^�[��Ԃ̓_�A����̓_�̓c�C�X�^�[��Ԃ̐��ɑΉ����܂��B�u�_�Ɛ��v�̊W�ł��B
�\�j�[�̈�[�厁�́A�悭�u�f�J���g����v�ƌ����Ă��������ł��B
�f�J���g���W��̓_�̓c�C�X�^�[��Ԃ̐��ŕ\�����Ƃ������ƂɃ��W���[�y�����[�Y�͋C�Â��܂����B
�F���̎d�g�݂̒T���ӂƂ���y�����[�Y�Y�����A�ЂƂ�ǓƂɑ{���𑱂��A�^�Ɛl�ɔ������u�Ԃł����B
�f�J���g���W�i�������̎���j��̓d�����d�q��́A�G�l���M�[�^���ʋ�ԏ�̏�ƁA�t�[���G�ϕ��i�t�[���G�ϊ��j�Ō���Ă��܂����A
�f�J���g���W�i�������̎���j��̓d�����d�q��́A�c�C�X�^�[��ԏ�̏�i�c�C�X�^�[���j�ƁA����ϕ��Ō���Ă��܂��B
�c�C�X�^�[���W��ɋL�q�����c�C�X�^�[��������ϕ�����ƁA�������̎����̃X�s�m�[����ɂȂ�܂��B
�d�����A���ʂ̂Ȃ��d�q��i�f�B���b�N���m=0�Ƃ������C����j�́A�����ʎ��R��̕����������A���̉��̓X�s�m�[����ɂȂ�܂��̂ŁA�����ʎ��R��i����̓X�s�m�[����ł��邪�j�́A�c�C�X�^�[��ԏ�̃c�C�X�^�[��������ϕ����邱�Ƃɂ���āA��ʓI�ɋ��߂邱�Ƃ��ł��܂��B
�����āA�f�J���g���Wx�̓c�C�X�^�[���W��=(��,��)�ƁA��=ix�ɂƂ����W�Ō���Ă��܂��B
�܂�A�������̎����̓_�́A��̃X�s�m�[���ŕ\����܂��B
�d����i���j�AKlein-Gordon��i�Β��Ԏq�j�A�f�B���b�N��i�d�q�A�z�q�A�����q�j�́A����̏�ɋL�q�����u��v�ł���܂������A��݂̂Ȃ炸�A���̂��̂��X�s�m�[���ŋL�q�����Ƃ����̂́A��ϋ����[�������ł��B
�X�s�m�[���A����͂Q��]������ƌ��ɖ߂�\���A�����Ă���͉����Ɍq�����Ă���Ƃ����\���Ȃ̂ł��B
|
|
|
|
|
2006/9/12�@���Θ_�ƃG�b�V���[�Ƒo�Ȑ�
|
|
���u���[�����c�ϊ��́A�������̈Ⴄ���ƂƁA���̊W�ł͂Ȃ����Ƃ�x�O������A���[�N���b�h�w�ɂ����镹�i����щ�]�ϊ��Ɠ���ł���B�v���Θ_�̈Ӗ��i�A�C���V���^�C�����A��g���X�jp34��蔲��
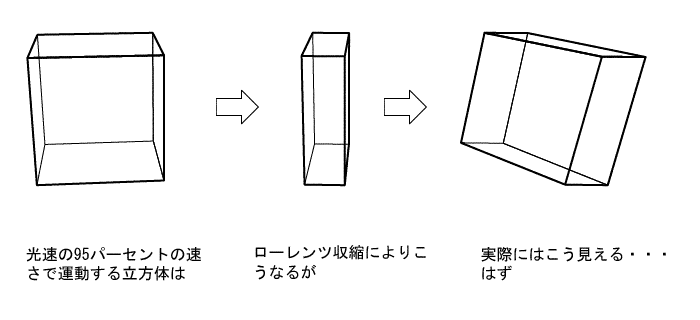
�����ꑊ�ΐ����_�ł́A�����ɋߕt���ƁA�����͏k�ނƌ����܂����A�����Ɍ����ƁA��]���Ă˂����Ƃ������Ƃ��Ӗ����Ă��܂��B�����̂��ڂ̑O��ʉ߂��鎞�A�ᑬ�ł͑��ʂ����������܂����A�����ɋߕt���ƁA���ʂ̂ق��ɁA���̖ʂ������Ă��܂��B����́A�˂���Ă��邱�Ƃ��Ӗ����܂��B
���X�s�m�[����̓`�d�́A���i�Ƌ�ԉ�]�ł���i�����^���j�B
��Dirac�������i�X�s�m�[����̕������j�́A�g���������̕���������������̂ł���B
���g��������
�g���������́A�o�Ȍ^�Δ����������ƌĂ��B
������A�V�����f�B���K�[�������́A�����^�Δ����������ł���B
���ԂɊւ��Ĉ�K�̕��f�Δ����������̂��߁A���̉��́A�O�p���ie^ix = cosx + isinx �j�̂������ɂȂ�B
�����[�����c�ϊ��̕s�ϗʂ͐��E���̒���
s^2 = x^2 + y^2 + z^2 - t^2
�ł���B
���Ԃ��}�C�i�X�œ����Ă���i�s�^�S���X�̒藝�ŁAt �� it�ɒu�������邱�Ƃɑ����j�B
���o�H�ϕ��Ɠ��v�͊w
�o�H�ϕ��Ŏ��Ԃ�t �� it�ɒu��������Ɠ��v�͊w�ɂȂ�B
���~�̎�
x^2 + y^2 = 1
���o�Ȑ��̎�
x^2 - y^2 = 1
y���}�C�i�X�œ����Ă���i�~�̎��ŁAy �� iy�ɒu�������邱�Ƃɑ����j�B
���O�p��
e^ix = cosx + isinx �� (cosx)^2 + (sinx)^2 = 1
���o�Ȑ���
e^x = coshx + sinhx �� (coshx)^2 - (sinhx)^2 = 1
���O�p���Ƒo�Ȑ����Ƃ̊W
coshx = cos(ix)
sinhx = -isin(ix)
�O�p���Ŋp�x�������ɂ���ix �� ix�j�ƁA�o�Ȑ����ɂȂ�B
�����[�N���b�h�w�ƃ��o�`�F�t�X�L�[�w
�����o�`�F�t�X�L�[�w
�o�Ȋw�Ƃ������B
�����o�`�F�t�X�L�[�w�ƃG�b�V���[
�G�b�V���[�́u�~�̋Ɍ��v�̓��o�`�F�t�X�L�[�w�ŕ`����Ă���B
 �@�@ �@�@
���o�Ȋw�̕����I�Ӗ�
�����w�I�ȑo�Ȋw�ɂ�肱��������̐��E�ɉ��p���邱�Ƃ��ł���B �����ʼn�]����~�Տ�ł̓��[�����c���k�ɂ�蕨�̂̒������k�ށB���̂Ƃ��~�Ղ̒��S���牓������ɂ�ĉ�]���x�������Ȃ邽�߁A�[�ɍs���قǃ��[�����c���k�̌��ʂ������o�邱�ƂɂȂ�B���̂悤�ȏꍇ�ł͓�_�Ԃ����ԍŒZ������(�~�Ղ̒��a���̂�����)��]�̒x�����S���̐��ɂȂ�~�܂�����Ԃ̉~�Ղ��猩��ƋȐ��ɂȂ�B�܂荂���ʼn~�Ղ���]���������߂ɒ������Ȃ���3�����̋�Ԃ����̋ȗ����������̂ł���B
���G�b�V���[�́u�~�̋Ɍ��v
�G�b�V���[�̍�i�u�~�̋Ɍ� I�v���悭����ƁA���̔w�������Ԑ��́A��������~���ɒ�������~�ʂō\������Ă��邱�Ƃ��킩��ł��傤�B

�O�p���̑o�Ȑ���
���[�N���b�h�w�̃��o�`�F�t�X�L�[�w�i�o�Ȋw�j
�ʎq�_�̑��Θ_
�̊W���C�ɂȂ��Ă��܂��B
�c�C�X�^�[���Ă���ȃC���[�W�Ȃ̂ł͂Ȃ��낤���H

�������̎���́A����Ȃ��̂ŏo���Ă���̂ł��낤���H

|
|
|
|
|
2006/9/16�@�Ȃ���Ԃ͎O�����Ȃ̂��H
|
|

���̎ʐ^�A���̒��ň�i�ƌ����Ă��锒���_�Z�ō����Z�p�`�ɒ��ڂ��Ă��������B���̘Z�p�`���悭���Ă���ƁA�c�����̂Ɍ����Ă��܂��B�܂�ŁA���Θ_�Ŗڂ̑O��ʉ߂��Ă䂭�c�����̂̂悤�ȁB
�����̌�_�ŁA����̓_����`����Ă���H
�c�C�X�^�[�̌����ɂ���āA����̓_����`�����H
�c�C�X�^�[�ɂ́A���A���A�[���̃w���V�e�B�[������܂��B
�w���V�e�B�[�Ƃ͂˂���̓x������\���܂��B
�w���V�e�B�[���[���̃c�C�X�^�[�́A�������̂��̂ł��B
���̃w���V�e�B�[�͉E�����A���̃w���V�e�B�[�͍������ł��B
���S������ˏ�Ɋg���钼���ƁA�������ƉE�����̋Ȑ��B
���̎ʐ^�ɂ́A���̎O�̃w���V�e�B�[���S�ĕ\������Ă��邱�ƂɂȂ�܂��B
��Ԃ��O�����Ȃ̂́A�c�C�X�^�[�ɎO�̃w���V�e�B�[�i���A���A�[���j�����邩��Ȃ̂��H
�c�����̂̏c�A���A�������A���ꂼ��A���S������ˏ�Ɋg���钼���ƁA�������̋Ȑ��A�E�����̋Ȑ��ɑΉ����Ă��邱�Ƃ��킩��܂��B
�����āA���S���痣���قǘc�����̂͑傫���Ȃ��Ă䂫�܂��B���ꂪ���Ԃ̌o�߂ɑΉ�����悤�Ɍ����܂��B
|
|
|
|
|
2006/9/23�@�_���n��Y�ꂽ����
|
|
***************�@�n���L�@**************
1 ���߂ɐ_�͓V�ƒn��n�����ꂽ�B
2 ���āC�n�͌`���Ȃ��C�r���Ƃ��Ă��āC�ł����̐[�݂̕\�ɂ������B�����āC�_�̊�������͂����̕\���s���߂����Ă����B
3 ���ꂩ��_�͌���ꂽ�C�u����������悤�Ɂv�B����ƌ�������悤�ɂȂ����B 4 ���̂̂��_�͌���ǂ��Ƃ����ɂȂ����B�����Đ_�͌��ƈłƂ̋敪��݂���ꂽ�B 5 �����Đ_�͌����g���h�ƌĂԂ��Ƃɂ��C�ł̂ق����g��h�ƌĂꂽ�B�������ė[�ƂȂ�C���ƂȂ����B����ڂł���B
6 �����Ő_�͌���ꂽ�C�u���̊Ԃɑ�����C���Ɛ��Ƃ̊Ԃɋ敪���ł���悤�Ɂv�B 7 �������Đ_�͑���C���̉��ɗ��鐅�Ƒ��̏���ɗ��鐅�Ƃ��敪���Ă䂩�ꂽ�B�����Ă��̂悤�ɂȂ����B 8 �����Đ_�͑����g�V�h�ƌĂԂ��Ƃɂ��ꂽ�B
�������ė[�ƂȂ�C���ƂȂ����B����ڂł���B
������
****************************************
����̓c�C�X�^�[�łł��Ă���B
�c�C�X�^�[�͓�̃X�s�m�[���łł��Ă���B
���͓�̃X�s�m�[���łł��Ă���B
�n���L���������Ƃ���A�_�͂ǂ����X�s�m�[����n��Y�ꂽ�悤�ł���B
�V�n������O�ɑn��Ȃ���Ȃ�Ȃ������͂��ł���B
���́A�O��ނ̃c�C�X�^�[�̂����̂ЂƂɉ߂��܂��A���̃c�C�X�^�[���X�s�m�[���Ƃ������w�I�\�������g����ł��Ă���̂ł�����B
�o�`�J�����M�������悤�Ƃ��Ă���u�����̒��ɏo�Ă���_�v���A��ԍŏ��ɍ�������̂ɂ́A���͍ޗ������݂��Ă������ƂɂȂ�܂��B
�o�`�J�����M�������悤�Ƃ��Ă��鏑���̒��ɏo�Ă���u�_�v�́A���ׂĂ̑n����ł���ɂ�������炸�A�������ǂ������炱������Ǝd����Ă��Ă���킯�ł��B
�܂��A����N�O�̐l�X���l�����F���ςł�����A�����������ƋC�Â������Ǝ��̂����ς�ł͂���̂ł����A���f���Ƃ��Ă͐���������܂���B
�X�s�m�[���͉����Ɍq�����Ă��邱�Ƃ�\�����w�I�\���ł�����A�W�������d�v�����������̉��N�̂ق����A�D�ꂽ�F���ςȂ̂�������܂���B
���͏@�����r�ł��闧��ł͂���܂��A�����I�F���ς̂ق������J�ł���悤�Ȉ�ۂ������Ă��܂��B
|
|
|
|
|
2006/9/23�@���C���̌��A�ƃR�C���̃X�s�m�[���B
|
|
4�̕��������}2�ł���悤�ɁA���̕������Ƃ����T�O������܂��B
���̌��̕��������X�s�m�[���ł��B
�d����i���j�̕������̕��������Ƃ�ƁA�X�s�m�[����̕������ɂȂ�܂��B
���������Ƃ�O�����C���ŁA���������Ƃ�ƃR�C���ɂȂ�܂��B
���邢�́A�R�C�����悷��ƃ��C���ɂȂ�Ƃ����C���[�W�ł��B
���C���Ƃ����̂́A���͍��i�����̓��������Ă��������Ă���̂ł����A�C���[�W�Ƃ��Ă̓s�G���̖X�q�̂悤�ȉ~�������������A�X�q�̒��_���珇�Ԃɗ�ɂ��Ă䂭�ƁA�������~�Ղ���傫���~�Ղ܂ł����т܂��B
���̉~�Ղ̒��S�����Ԃƃ��C���ɂȂ�܂��B�i�~���R�t�X�L�[�̌��~���ƌ������ق���������₷���ł��傤���B�j
����A�R�C���Ƃ����̂́A���L�̐����̃C���[�W�Ȃ̂ł����A�q���̂���̊��L�̓�����͏����ȉ~�ł����A��������ɏ]���ē�����͑傫�ȉ~�ɂȂ�܂��B
���̉~�̒��S�����ԂƃR�C���ɂȂ�܂��B�������̂ڏĂ��ŁA�Ђ˂�Ȃ��Ɛg���o�Ă��Ȃ��悤�Ȃ��̂ł��B
�����āA���̏����ȉ~����傫�ȉ~�ւ̓������A���Ԃ̗���ŁA���̏ꍇ�́A�r�̔g��̂悤�ɓ��S�~��i�ق�Ƃ͎l�����Ȃ̂œ��S����j�ɍL�����Ă䂫�܂����A�X�s�m�[���̏ꍇ�́A���L�̂悤�Ƀc�C�X�g���Ȃ���L�����Ă䂭�`�ɂȂ�܂��B�i�~���R�t�X�L�[�̌��~�����˂������悤�Ȃ��́B�j
�E�����̊��L�ƍ������̊��L���������킹�܂��Ɓi���������Ƃ����Ӗ��ł͂Ȃ��j�A�������Ȃ��L�����܂��킯�ł��B
��قǂ͊ȒP�̂��߂ɁA�R�C�����悷��ƃ��C���ɂȂ�Ɛ\���܂������A�X�s�m�[���͕��f���̐��E�ł��̂ŁA���m�ɐ\���グ�܂��ƁA���f�������Ƃ��Ċ|�����킹�邱�ƂɂȂ�܂��B
�E�����X�s�m�[���̕��f�������Ƃ�܂��ƍ������X�s�m�[���ɂȂ�܂��̂ŁA�E�����X�s�m�[���ƍ������X�s�m�[�����������킹�܂��ƁA�����Ȃ��X�s�m�[���܂�������܂��킯�ł��B
�i�����I�ɂ́A�f�B���b�N�������̉��Z�q�ƁA����̕��f�������Ƃ������̂��|�����킹��ƁA�g���������̉��Z�q�i�_�����x���V�A���j�ɂȂ�Ƃ������Ƃł��B���f�������Ƃ�ƌ����܂����������Ɛ��m�ɂ́A��]�̕�����ς��A���i�̕������ς���Ƃ������Ƃł��B�j
��̔��������؋��̎ʐ^�ŁA�k�ɂ���ԓ������ɐL�т�O�{�ׂ̗荇�����o���i�n���̌o�x�ɑ���������j�ƁA�O�{�ׂ̗荇���Ċ����オ�闆���ƁA�O�{�ׂ̗荇���Ċ��������闆���ɒ��ڂ��Ă݂Ă��������B
��[���z���͂����Ȃ���A���Ă��܂��ƁA
�k�ɂ���ԓ������ɐL�т�O�{�ׂ̗荇�����o���̂Ȃ��ɁA�g�債�Ă䂭�����̂������܂��B
�܂��A�O�{�ׂ̗荇���Ċ����オ�闆���̒��ɁA�˂���Ȃ��犪���オ���Ă䂭�c�����̂������܂��B������ԓ��Ɍ������ɏ]���Ċg�債�Ă䂫�܂��B
����ɁA�O�{�ׂ̗荇���Ċ��������闆���̒��ɁA�˂���Ȃ��犪���������Ă䂭�c�����̂������܂��B������ԓ��Ɍ������ɏ]���Ċg�債�Ă䂫�܂��B
����ɑz���͂����āA�����̗����̂ɓ��ڂ��鋅��z�����Ă݂ĉ������B
�����܂������H���̋����z���ł������ǂ������d�v�ł��B
�o���i�n���̌o�x�ɑ���������j�ɉ����āA�g�債�Ă䂭���̋��ʂ̓������A���̔g�̓`�d��\���Ă��܂��B�i�܂�~���R�t�X�L�[�̌��~���̎l�����łł��B�j
�܂��A�����オ���Ă䂭�����ɉ����ăc�C�X�g���Ȃ���g�債�Ă䂭���ʂ��A�E�����X�s�m�[���̔g�ʂ̓`�d�������ɕ\���Ă��܂��B
���l�ɁA�����������Ă䂭�����ɉ����ăc�C�X�g���Ȃ���g�債�Ă䂭���ʂ��A�������X�s�m�[���̔g�ʂ̓`�d�ł��B
���̎ʐ^�̓c�C�X�^�[���C���[�W���邽�߂ɓY�t�������̂ł����A�X�s�m�[���̔g�̓`�d���C���[�W����̂ɂ���ϖ𗧂��܂��B
|
|
|
|
|
|
���؋��̒��Ɍ����邠�̗����̂́A�����炭����ł��傤�B
���Θ_�̘c������悭�\�����Ă���Ǝv���܂��B
�O�{�̃c�C�X�^�[�i�o���A�E���Ɋ����オ���Ă䂭���A�������Ɋ����������Ă䂭���j����Ԃ̏c�A���A�����ɑΉ����Ă���悤�Ɍ��Ă��܂��B
�l�{�̃c�C�X�^�[���邢�̓X�s�m�[������Ȃ閳���̊i�q���F���ɒ���߂��炳��Ă���Ƒz�����܂����B
�V���ǂ��c�C�X�^�[�łł��Ă���c�C�X�^�[���[���[�R�[�X�^�[�ɏ���āA�Q���������Ԃ̒���˂��i��ł䂭�̂��������̎���ł���Ƒz�����܂����B
�܂��A���̐}�ł́A�c�C�X�^�[��{���B��Ă���Ƒz�����܂����B
�k�ɂ���ԓ��Ɏ���o���́A��{�Ɍ����܂����A���͓�{����ƁB
����͎l���������̂�`���Ă݂āA�������]�����Ă݂�ƕ�����̂ł��B
�o���́A�~�ʂɌ����܂����A���́A��C�̎ւ����ݕt���Ă���悤�ɂȂ��Ă��܂��B
�T�C���J�[�u�ƃR�T�C���J�[�u���ꏏ�̃O���t�ɏ������悤�ɂȂ��Ă��܂��B
�����̎����Ƃ���ɂ��A��_�̎��ɂ��F�����h��A�ߋ������������̒��ɐ܂肽���܂�Ă���ƌ������Ƃł��B
�،��o�̉F���ςł��B
�����Ă��܂��A���̖��؋��̓�ɂ͂ǂ��Ȃ��Ă���̂ł��傤���B�����k�ɂƓ����悤�ɂȂ��Ă�����B�B�B
�������Ԃ��ŏI�I�Ɉ�_�ɏ�ݍ��܂��̂ł́B�B�B�{���̂��Ƃ��Q�̒��ɁB�B�B�܂��Ɉ�H�̎��ɏh��S�F���B
����ȑz���܂ł��Ă݂܂����B
|
|
|
|
|
2006/9/23�@��̃X�s�m�[���ƁA�d�q�A�z�d�q���C���[�W����B
|
|
���C���̐��������Ă��Ă��������B�ڂɎh����Ȃ��悤�ɂƂ������ق�����O�Ɍ����Ċ���������Ă݂܂��ƁA��O���牜�ɉE�����܂莞�v���Ɋ����Ă���Ǝv���܂��B
���̐����g���ă��C���̃R���N�����̂��Ƃ��l���Ă݂܂��傤�B
�@�܂��A�����R���N�ɂ����āA����O�����ɂЂ˂�Ȃ���R���N�ɐ����������݂܂��B
�A�R���N���r�����甲������A�R���N������Ȃ��獡�x�́A���������ɂЂ˂�Ȃ���R���N��������͂����܂��B
���̒��ɁA�������̃��C���̐����������Ƃ��܂��B�i�E�����̂��̂Ɋ���Ă��鎄�����ɂ͂����炭���̂������g���ɂ����ł��傤���B�j
���̐��̏ꍇ�͂ǂ̂悤�Ɏg�����ƂɂȂ�ł��傤���B
�B���ɃR���N�������āA���������ɂЂ˂�Ȃ���R���N�ɐ����������݂܂��B
�C�R���N���r�����甲������A�R���N������Ȃ��獡�x�́A����O�����ɂЂ˂�Ȃ���R���N��������͂����܂��B
�g������Ă���E�����̃��C���̐����A�E�����̃X�s�m�[���ł��B������X�s���AUp�X�s���̃X�s�m�[���ȂǂƂ������܂��B
�g�����炢�������̃��C���̐����A�������̃X�s�m�[���ł��B�������X�s���ADown�X�s���̃X�s�m�[���ȂǂƂ������܂��B
�E�����̃��C���̐����d�q�ŁA�������̃��C���̐����z�d�q�A�ł͎��͖����̂ł��B
�E�����̃��C���̐��̂����A�@�̏�ԁA�܂荷�����݂��鎞�̏�Ԃ��d�q�i������X�s���̓d�q�j�ŁA
�A�̏�ԁA�܂�����R���N����͂��������Ԃ��z�d�q�i������X�s���̗z�d�q�j�ł��B
�����I�ɂ͓����E�����̐��Ȃ̂ł����A�R���N�ɑ���i�s�����Ɛ����̂̉�]�������قȂ�܂��B
�܂��A
�������̃��C���̐��̂����A�B�̏�ԁA�܂荷�����݂��鎞�̏�Ԃ��d�q�i�������X�s���̓d�q�j�ŁA
�C�̏�ԁA�܂�����R���N����͂��������Ԃ��z�d�q�i�������X�s���̗z�d�q�j�ł��B
�z�d�q�𗝘_�I�ɗ\�������̂̓f�B���b�N�ł����A�z�C�[���[�ƃt�@�C���}���͗z�d�q�ɂ��ĉߌ��ȉ��߂̎d������܂����B
�z�d�q�́u���Ԃ������̂ڂ�d�q�ł���v�ƁI�B
�ߋ����疢���������z�d�q�́A��������ߋ��������d�q�Ƃ܂����������Ȃ̂ł��I
�����E�����̃��C���̐��ŁA�R���N�ɑ���i�s�������قȂ�A�Ƃ������b�����܂������A ����͎��Ԃɑ���i�s�������قȂ��Ă��邱�Ƃ̚g���������̂ł��B
�܂���́A�@�i������X�s���̓d�q�j�ƇC�i�������X�s���̗z�d�q�A���邢�͉������X�s���̎��Ԃ������̂ڂ�d�q�ƌ����Ă��ǂ��j����ł��Ă���̂ł��i�܂��͇A�ƇB�j�B
���ꂪ�d�q�Ɨz�d�q�̑ΐ����A�Ώ��łł��B
|
|
|
|
|
2006/10/15�@�����ԁA�����ԂƓ�d�X���b�g�̎���
|
|
����܂Ŏ���́A�c�A���A�����A���Ԃ�4�����ł���Ǝv�������Ă��܂������A������������A���Ԃɂ͎����ԂƂ͕ʂɋ����Ԃ����邩������܂���B
�ʏ�̎��Ԃƒ��p�Ɍ�����Ă��鋕�����Ԃł��B
�i���w�ŕ��f�����A�������Ƌ����������p�Ɍ������W��Ƀv���b�g����悤�ɁA�������Ԃ͎������Ԃƒ��p�Ɍ�����Ă��܂��B�j
�c�A���A�����̋�Ԃ̂Ȃ����A���ۂ͎��ԕ����i��ł䂫�܂����A�������ۂ��A�����ԕ����Ƌ������ԕ������璭�߂邱�Ƃ��ł��܂��B
�ʎq�_�̗��q���Ɣg�����̑���́A�������ۂ����̂悤�Ɏ����ԕ����Ƌ����ԕ������猩�����̂Ƃ��ĉ��߂��ł������ł��B
�����ԕ������猩��Ɨ��q�Ɍ����鎖�ۂ��A�����ԕ�������͔g���Ɍ�����Ƃ����킯�ł��B
2006/9/16�̓��L�ł��Љ����̖��؋��ŁA�o�������ԂɌ����āA�����̂��o�������Ɉړ����Ă䂭�i�܂��Ԃ����ԕ����Ɉړ����Ă䂭�j�Ƃ������b�����܂������A���̖��؋��Ōo�������ԂɌ����Ă܂��ƁA�o�x0�x�̌o���ƁA�o�x90�x�̌o���͖k�ɂŒ������Ă��܂��i���̖��؋��ł͌o����16�{����܂��̂ŁA4�{�ׂ�̌o���͂��Ƃ̌o���Ɩk�ɂŒ��p�Ɍ�����Ă��܂��j�B
���̌o�x0�x�̌o���������ԁA�o�x90�x�̌o���������Ԃł͂Ȃ����Ǝv���܂����B
�����Ėk�ɂƂ�����_���狅��ɍL����A�܂���ɂƂ�����_�Ɏ��k���܂��B
�ł́A�����ԂƋ����Ԃ̃C���[�W�����Ă݂܂��傤�B
���𐳖ʂ��猩�܂��ƁA�c�Ɖ��ɍL���������̂Ƃ��Č����܂��B
���_�����炵�đ��ʂ��猩�Ă݂܂��ƁA�����̂Ȃ����Ƃ��������܂���B
���ʂ��猩��Ɠ��Ɍ����Ă������̂��A���_��90�x���炵�đ��ʂ��猩�邱�Ƃɂ��A�ꎟ���ɂȂ��Ă��܂��܂��B
�Ⴆ�A���ʂ��猩���ꍇ�������ԕ����A���ʂ��猩���ꍇ�������ԕ����A�ƍl���邱�Ƃ��ł��܂��B
���ʂ��猩���ꍇ�ɂ͍L���肪���������̂��A���ʂ��猩��Ƃ��̍L���肪�Ȃ��Ȃ�܂��B
�܂�ˉe���ꂽ�Ƃ������Ƃł��B
���t��ς���A�����ԕ����ł͍L���肪���������̂��A�����ԕ����ł͍L���肪�Ȃ��Ȃ�B
�����ԕ����Ō����Ă�����̂́A�����ԕ����ōs���Ă��邱�Ƃ̎ˉe�ł���A�Ƃ������Ƃł��B
��̖��؋��ɗ����߂�A���ɉ��т�o���������ԁA�^��ɉ��т�o���������Ԃƍl���Č��܂��傤�B
���ɉ��т�o���ɉ����������̂́A�T�C�R���̂悤�ɂ�������Ƃ��������̂Ɍ����܂����A�^��ɉ��т�o���ɉ��������̂̓T�C�R�����Ԃ����l�ɝG���ȗ����̂Ɍ����܂��B
�����Ԃɉ����������̂́A�����ԂɎˉe����G���ɂȂ��Ă��܂��܂��B
�����ԕ����ɉ�������ԂŖL���ɌJ��L�����Ă��鎖�ۂ́A�����ԕ����ɉ�������Ԃł́A�e���������Ȃ��Ȃ��Ă��܂��܂��B
�����ԕ����ŖL���ɌJ��L�����Ă���g�����ۂ��A�����ԕ����Ɏˉe���ꂽ���ʁA���q�ɂ��������Ȃ��Ȃ��Ă���悤�ȋC�����Ă��܂��B
�u�|�e���V�����G�l���M�[�Ɖ،��\���v�̒��ł��Љ���悤�ɁA�����ԕ����ŋL�q�����o�H�ϕ��̔g�����́A�����ԕ����ł͓��v�͊w�ɕϊ�����܂��B
�����ԂŋL�q�����o�H�ϕ��͔g�����ۂ�\�킵�Ă��܂��B
���̎��Ԃ������Ԃɕϊ�����ƌ����ɓ��v�͊w�ɂȂ�܂����A���v�͊w�Ƃ́A�u���E���^��������ʎq�͊w�I���q�̓��v�I�^����\���������̂ł��B
�ʎq�_�ɂ�����g���Ɨ��q�̓�d���́A���̋����Ԃ�������Ԃւ̎ˉe�ŗ�������ƕ�����₷���悤�ȋC�����Ă��܂��B
��d�X���b�g�̎����ł́A�g�����̂��߂Ɋ��Ȃ��X�N���[����Ɍ�������ŁA�X�N���[����̋P�_�i���q���j�̓A�b�g�����_���ɋL�^����܂��B���̃A�b�g�����_�����̌������A�u���E���^���ł��B
�����Ԃ̔g�����Ǝ����Ԃ̗��q�����A�X�N���[���̏�œ����Ɋϑ������킯�ł��I
|
|
|