Dirac��̏�ݍ���
�g�����̎�v�`�͈�ʂɁA
![]()
�Ə����܂��B������![]() �͍�p�ŁA���O�����W���A�����x
�͍�p�ŁA���O�����W���A�����x![]() ��p����ƁA
��p����ƁA
![]()
�Ə������Ƃ��ł��܂��BDirac��̃��O�����W���A�����x�́A
![]()
�ł��B
����ADirac������
![]()
���ADirac��͈ȉ��̂悤�ɉ������Ƃ��ł��܂��B
![]()
�����ɁA![]() �́ADirac��̓`�d���ł��B
�́ADirac��̓`�d���ł��B
Dirac��̕��f�����́A
![]()
�ł��̂ŁA���O�����W���A�����x�́A�ȉ��̂悤�ɏ����܂��B
![]()
�]���܂��āA��p�́A
![]()
�ƂȂ�A�g�����́A
![]()
�ƂȂ�܂��B
���낢��ȏ�̍�p�̎�v���������Ő������Ă����܂��傤�B
�@Klein-Gordon��i�u���s����Ƒ��Θ_�I���q��v���Q�Ɓj
![]()
�ADirac��
![]()
�B�d����i�u���̎��Ƃ́v���Q�Ɓj
![]()
���邢��
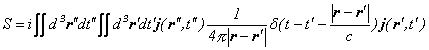
�C�d�͏�i�u�}�b�n�̌����v���Q�Ɓj
![]()
�@�`�C�܂Ō���ׂĂ݂܂��ƁA�ǂ̏���݂��ƂɁA
![]()
�̌`�ɂȂ��Ă��邱�Ƃ��A�킩��܂��B
![]() �́A�g�̔g���̐U����\���A
�́A�g�̔g���̐U����\���A![]() �́A�g��
�́A�g��![]() ����n�_
����n�_![]() �܂ł̔g�̓`�d��\���Ă��܂��B
�܂ł̔g�̓`�d��\���Ă��܂��B
�g��![]() �̐U�����A�g
�̐U�����A�g![]() ��ʂ��āA�n�_
��ʂ��āA�n�_![]() �ɏ�ݍ��܂�܂��B
�ɏ�ݍ��܂�܂��B
�S�Ă�![]() �̉e�����A�n�_
�̉e�����A�n�_![]() �ɏ�ݍ��܂�܂��B
�ɏ�ݍ��܂�܂��B
���ꂪ�A�f�r�b�h�E�{�[���̃z���O���t�B�b�N�F����A�،��o�́u��H�̎�����F�����h���A��u�̐��̂܂������ɉi���̎��Ԃ��Ïk����Ă���v�̐��w�I�\���Ȃ̂�������܂���B
�g![]() �́A�d���g�ł���A�d�͔g�ł���A�����g�ł�������̂ł��B
�́A�d���g�ł���A�d�͔g�ł���A�����g�ł�������̂ł��B
�܂�A�����g�iDirac��j�̏ꍇ�A�������̂��̂��A�����ɏ�ݍ��܂��̂ł��B
�ߋ��̕����������̕������A�����đS�F���̕������A�u���v�����āu�����v�Ƃ����ꏊ�ɏ�ݍ��܂�Ă���̂ł��B
�d����̏ꍇ�́A�g�͌��ł��̂ŁA�F����Ԃ̐��X����o�������A�������̖ڂ̒��ɏ�ݍ��܂�܂��B���ꂪ�u����v�Ƃ������Ƃł��i�u�B���I���R�Ȋw�ς̔ے�v���Q�Ɓj�B
Dirac��̏ꍇ�́A�g�͕����g�ł��̂ŁA�F����Ԃ̕������̂��̂��A��H�̎���A�ь��̒��ɏ�ݍ��܂��킯�ł��I�i����͋����̎����ł��B�j
���̏�ݍ��܂ꂽ���̂�
![]()
�ƒu���Ă݂܂��ƁA
![]()
�ƂȂ�܂��̂ŁA�����ɏ�ݍ��܂ꂽ����![]() �ƁA�����ɂ���������
�ƁA�����ɂ���������![]() �Ƃ̑��ݍ�p��S�Ă�
�Ƃ̑��ݍ�p��S�Ă�![]() �ɂ��đ������킹��ƁA�S��p�ɂȂ�̂ł��B
�ɂ��đ������킹��ƁA�S��p�ɂȂ�̂ł��B
���̍�p���ŏ��ƂȂ�Ƃ���݂̂����ۂƂ��Č���܂��i���ꂪ�o�H�ϕ��̐^���j�B
���ۂ̌�����̌������邱�̍�p�̎����A�z���O���t�B�b�N�\���A�������͉،��\���ɂȂ��Ă���Ƃ������Ƃ́A�Ȃ�Ƃ������ł͂���܂��I