Dirac方程式の伝播関数

前回、「相対論的電子場の方程式（Dirac方程式）」の中で、Dirac方程式は、

や

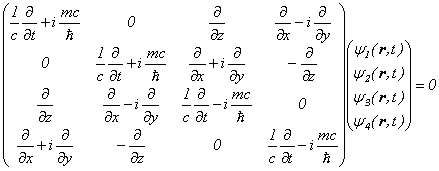
という形で書けることをお話しました。

Dirac方程式の伝播関数は、この行列の逆行列の形で形式的に表すことができます。

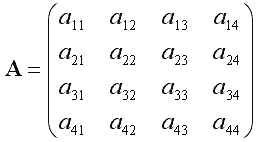
について

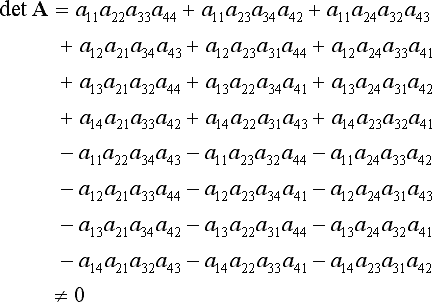
のときAの逆行列が存在して

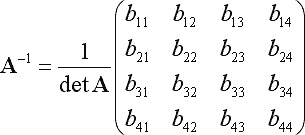
ただし

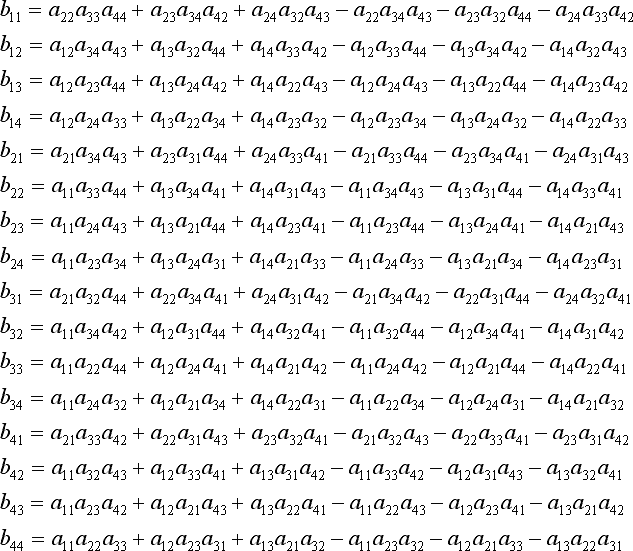
ですので、ここで

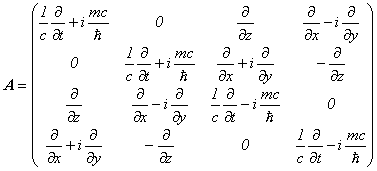
について、行列式を計算してみますと

に注意して、

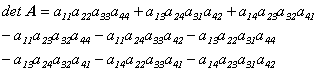
となります。また

に注意いたしますと、

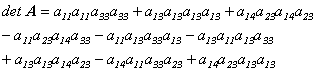
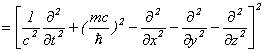
と計算できます。

次に各行列要素を計算してみますと

に注意して、

となります。具体的に要素を代入してみますと、

･･････

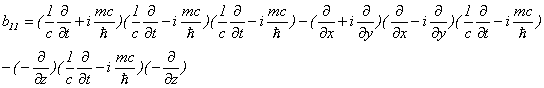
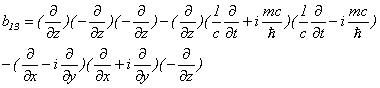
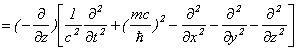
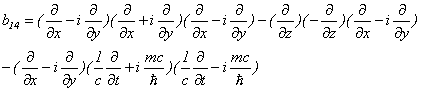
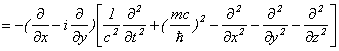
のように計算できます。従いまして、Dirac方程式の伝播関数は形式的に

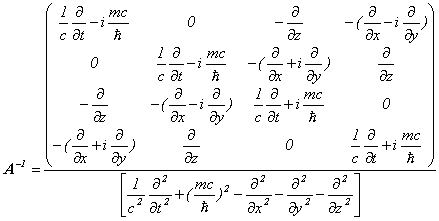
となります。

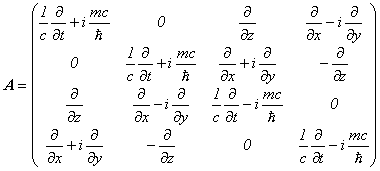
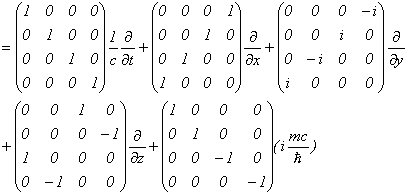
でしたので、Dirac方程式の伝播関数は、

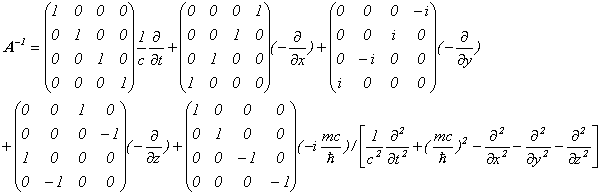
とも書けます。

Dirac方程式

に対して、伝播関数は形式的に、

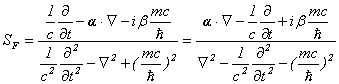
と書けるというわけです。

また、Klein-Gordon方程式の伝播関数は、形式的に

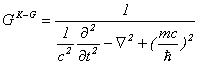
と書けますので、Dirac方程式の伝播関数は、

とも書くことができます。

Klein-Gordon場や電磁場は、何とか日本語（言葉）で説明することができますが、このDirac場（スピノール場）は、もはや言葉での表現を超えた世界です。

真実をより深く知ろうとするためには、どうも言葉という道具だけでは不十分のようです。

数式にしてみて、初めてその意味を知ることができる世界があるようです。

そしてそれらは、電子や陽子、中性子を表すDirac場であり、私たちはこれらから出来ているのですから、何とも不思議です。

それでも無理をして言葉で説明してみますと、なんとか以下のようになります。

電子や陽子、中性子の世界は４つの波でできています。

つまり、、、、です。

そして、この４つの波とは、時間の２つの方向、つまり「過去から未来」と「未来から過去」の２つと、螺旋状に回転する波の回転方向、つまり「時計回り」なのか「反時計回り」なのかの２つに関係しています。

これらの４つの波が、絡み合った世界、それが私たちの世界なのです。