���Θ_�I�d�q��̕������iDirac�������j
����܂ŁA�g��������
![]()
�ő�\�����d�����Klein-Gordon������
![]()
�ő�\����鑊�Θ_�I���q��������Ă��܂������A�����͉�����{�[�Y���q�i�{�]���j�ƌĂ����̂ŁA���ꂾ���ł͐��̒��̔������������ł��Ă��܂���B���̒��ɂ̓{�[�Y���q�i�{�]���j�̂ق��ɁA�t�F���~���q�i�t�F���~�I���j�Ƃ������̂�����܂��B����͓d�q�ɑ�\����ADirac�������ɏ]���܂��B
|
�X�s�m�[�� |
�e���\�� |
�X�s�� |
|
��i�g���j |
���q |
|
0�K |
0�K |
0 |
�X�J���[ |
Klein-Gordon�� |
�{�]���i�Β��Ԏq�j |
|
1�K |
�| |
1/2 |
|
Dirac�� |
�t�F���~�I���i�d�q�A�z�q�A�����q�j |
|
2�K |
1�K |
1 |
�x�N�g�� |
�d���� |
�{�]���i���q�j |
|
3�K |
�| |
3/2 |
|
Rarita-Schwinger�� |
�t�F���~�I���i�d�͔��q�j |
|
4�K |
2�K |
2 |
|
�d�͏� |
�{�]���i�d�͎q�j |
Dirac�́AKlein-Gordon�����������Ԃɂ���1�K�ɂȂ�悤��Klein-Gordon�������̍��ӂ�2�K�������Z�q�̕��������Ƃ邱�Ƃ��l���܂����B
�������A�P���ȕ������ł�
![]()
�̂悤�ɁA�[�����������ƂȂ��Ă��܂��A�����Ȕ����������ɂ͂Ȃ�܂���B������Dirac�͕�������L�������Ă��܂����Ƃ������z�ɓ���܂����B�܂�A
![]()
�Ƃ���1�K�̔������Z�q���l���A�W��![]() ��
��
![]()
���P���I�ɐ��藧�悤�ɑI�Ԃ̂ł��B���ʁA���Ԃɂ���1�K�ƂȂ鑊�Θ_�I�Ȕg���������A
![]() ����@
����@
![]()
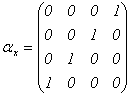 �@
�@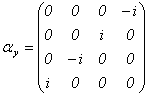
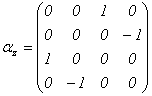 �@
�@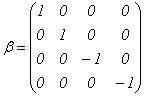
�������܂����B��������R�d�q��Dirac�������ƌĂт܂��B
�Ȃ��W��![]() �́A�p�E���̃X�s���s��
�́A�p�E���̃X�s���s��![]() ���g���ƁA
���g���ƁA
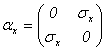 �@
�@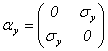 �@
�@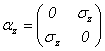
���Ȃ킿�A![]() �Ə����邱�Ƃɒ��ӂ��܂��傤�B
�Ə����邱�Ƃɒ��ӂ��܂��傤�B
�܂�́A�d�q�̃X�s���������AKlein-Gordon�̔g���������́u�������v���Ƃ邱�Ƃɂ���āA�g�������瓱���o�����Ƃ��ł��Ă��܂����킯�ł��B
���R�d�q��Dirac�������J�ɏ��������Ă݂܂��ƁA�E�ӑ�ꍀ�́A
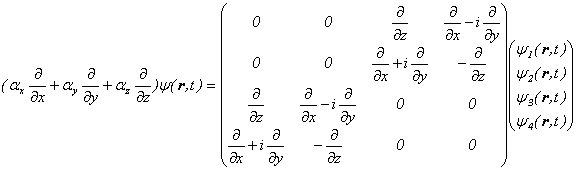
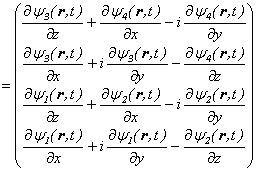
�ƂȂ�A�E�ӑ�́A
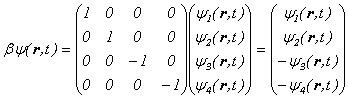
�ł��̂ŁA�ȉ��̂悤�Ȏl�g�̔g���������������܂��B
![]() ����A-1
����A-1
![]() ����A-2
����A-2
![]() ����A-3
����A-3
![]() ����A-4
����A-4
�����ŁA�@��
![]()
���`���I�ɉ����Ă݂܂��ƁA
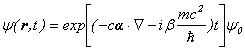
�ƂȂ�܂��B
����́A���̉��Z�q���A���Ԕ��W���Z�q�v���X��ԉ�]���Z�q�ɂȂ��Ă��邱�Ƃ�
�Ӗ����Ă��܂��B
�܂�A
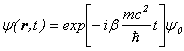
�̕��������Ԕ��W�����肵�A
![]()
�̕�������ԉ�]�����肵�܂��B
�Ⴆ�·A-1���ƇA-2�������킹�Ă݂Č��܂��ƁA
������![]() �ŕ\�����g�����x�N�g���́A���Ԃ𖢗������ɐi��ōs���܂����A������
�ŕ\�����g�����x�N�g���́A���Ԃ𖢗������ɐi��ōs���܂����A������![]() �ŕ\�����
�ŕ\�����![]() ���̎���Ɏ��v���̗�����ɉ�]���Ă���g�����x�N�g���Ɨ��ݍ����Ă���Ɠǂ߂܂��B
���̎���Ɏ��v���̗�����ɉ�]���Ă���g�����x�N�g���Ɨ��ݍ����Ă���Ɠǂ߂܂��B
�܂��A�A-3���ƇA-4�������킹�Ă݂Č��܂��ƁA
������![]() �ŕ\�����g�����x�N�g���́A���Ԃ��ߋ������ɐi��ōs���܂����A������
�ŕ\�����g�����x�N�g���́A���Ԃ��ߋ������ɐi��ōs���܂����A������![]() �ŕ\�����
�ŕ\�����![]() ���̎���ɔ����v���̗�����ɉ�]���Ă���g�����x�N�g���Ɨ��ݍ����Ă���Ɠǂ߂܂��B
���̎���ɔ����v���̗�����ɉ�]���Ă���g�����x�N�g���Ɨ��ݍ����Ă���Ɠǂ߂܂��B
���R�d�q�Ƃ́A���v���̗�����̔g�ƁA�����v���̗�����̔g�����ݍ����Ă�����̂Ƃ��ĕ\�������̂ł��B
�Q�l�܂łɇA�������낢��Ȍ`�ɕό`���Ă����܂��傤�B
���ӂ�![]() �Ŋ���ƁA
�Ŋ���ƁA
![]()
![]()
![]()
![]()
�ƂȂ�܂����A�K���Ɉڍ����Ă݂܂��ƁA
![]()
![]()
![]()
![]()
�Ƃ������܂��B����͍s��`���ŁA
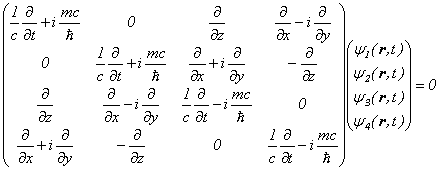
�Ƃ������܂��B