波動性と特殊相対性理論

相対論的粒子は、以下のようなKlein-Gordon方程式に従います。

Klein-Gordon方程式の伝播関数は以下のような形をしています。

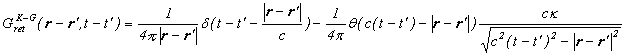
Bessel関数の漸近形を使うと、伝播関数は以下のような形になります。

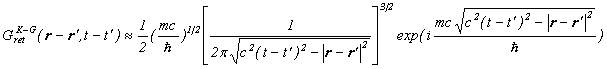
相対論的粒子の伝播関数（Klein-Gordon場）のある時刻の断面は、以下のようなグラフです。

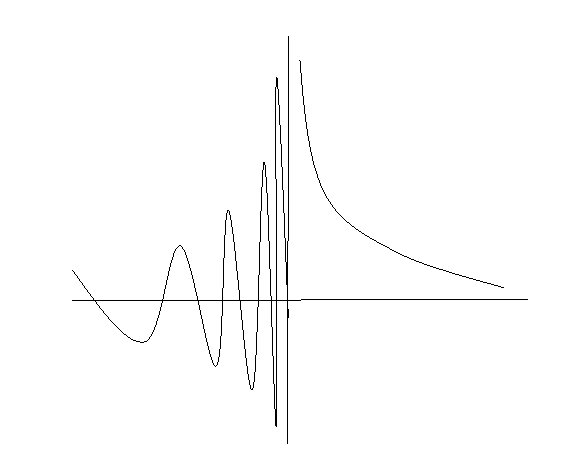
時空距離がゼロに近付くと、振幅が大きくなり、波長が短くなります。

つまり相対論的粒子は、速度が光速に近付くほど、振幅は大きくなり波長は短くなってきますので（波数は大きくなってゆきますので）、光速に近ければ近いほどミンコフスキーの光円錐付近に振幅が大量にたまってくることがわかります。

一方で、光子は、ミンコフスキーの光円錐上にしか振幅はありません。つまり、光子は常にミンコフスキーの光円錐上に存在しています。

ちなみに、光子の伝播関数（電磁場）は、

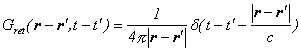
ですので、ある時刻の断面は以下のようなグラフになります。

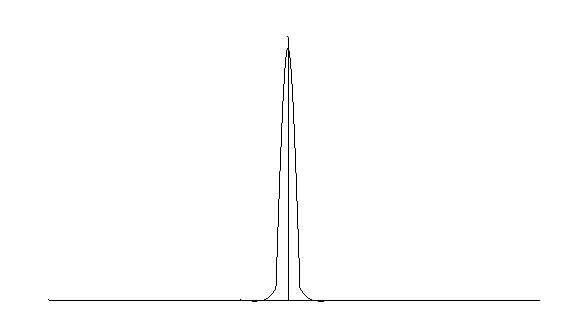
このように、Klein-Gordon方程式の伝播関数と、波動方程式の伝播関数を比べてみますと、大変興味深いです。

また、伝播関数の漸近形で、粒子の速度が遅い時には、

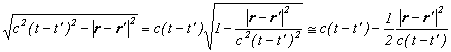
と近似できますので、伝播関数の漸近形は、

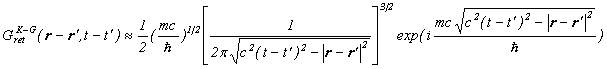
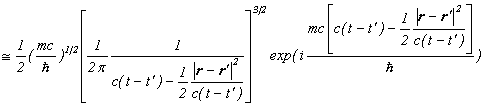
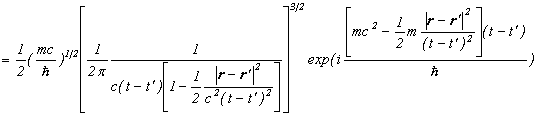
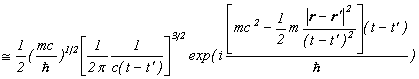
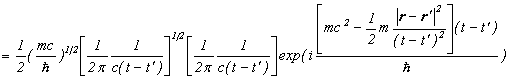
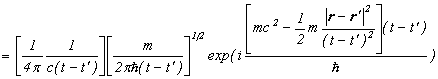
というように、シュレディンガー方程式の解になりますので、ある時刻の断面において伝播関数のグラフは、以下のような平面波になります。

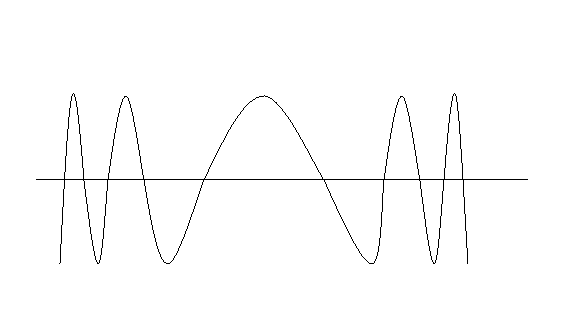
速度が遅い時は、伝播関数はこのような平面波なのですが、速度が速くなってくると、波がミンコフスキーの光円錐付近に押しやられてゆき、光円錐近傍に振幅がたまってゆく様子が、最初のグラフと比べるとわかります。

伝播関数の漸近形を見るとわかるように、Klein-Gordon場の作用は、

です。作用の空間微分は運動量で、作用の時間微分はエネルギーですので、

のように計算されまして、特殊相対性理論でおなじみの運動量とエネルギーが導けます。

従いまして、Klein-Gordon方程式の伝播関数は、以下のように変形できまして、

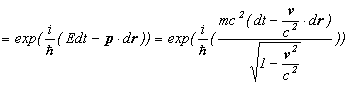
以前「特殊相対性理論と量子条件、そして経路積分」で述べた式が導出できます。

最後に、というものを計算してみますと、

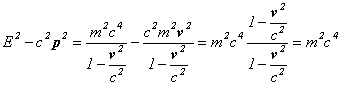
となって、おなじみの相対論的粒子のエネルギーと運動量の関係（分散関係）が出てきます。