経路積分からシュレディンガー方程式を導いてみる
すでに見てきたように、方程式
![]()
により時刻![]() における波動関数が時刻
における波動関数が時刻![]() における波動関数によって表されるということも見てきた。核
における波動関数によって表されるということも見てきた。核![]() は時間間隔
は時間間隔![]() に対する作用に
に対する作用に![]() を掛けたものの指数関数に比例する。短い時間間隔
を掛けたものの指数関数に比例する。短い時間間隔![]() に対して作用はこの時間間隔のラグランジュアンに
に対して作用はこの時間間隔のラグランジュアンに![]() を掛けたものによって近似できる。すなわち、
を掛けたものによって近似できる。すなわち、
![]() ・・・①
・・・①
が得られる。
1次元でポテンシャル![]() の中を運動する粒子の特別な場合、すなわち
の中を運動する粒子の特別な場合、すなわち
![]()
の場合に、この式を適用してみよう。この場合①は、
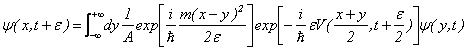
となる。最初の指数部分に![]() が現れる。
が現れる。![]() が
が![]() から有限だけ離れていると
から有限だけ離れていると
![]() は
は![]() で非常に大きくなるので指数因子
で非常に大きくなるので指数因子![]() は
は
![]() の変動に対して非常に急激に振動する。この因子が急激に振動するとき、
の変動に対して非常に急激に振動する。この因子が急激に振動するとき、![]() についての積分が非常に小さくなる(他の因子は緩やかに変動するので)。
についての積分が非常に小さくなる(他の因子は緩やかに変動するので)。![]() が
が![]() に近いときに限り(このとき指数因子はゆっくり変化する)、主要な寄与が得られる。この理由により、
に近いときに限り(このとき指数因子はゆっくり変化する)、主要な寄与が得られる。この理由により、
![]() とおくと
とおくと![]() が小さいところだけが積分の主要な寄与を与えるものと期待できるのである。代入すると
が小さいところだけが積分の主要な寄与を与えるものと期待できるのである。代入すると
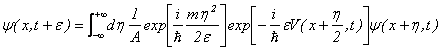
が得られる。最初の指数因子の位相は![]() が
が![]() の程度のときに1ラジアン程度変動するので、積分の主要な寄与はこの程度の
の程度のときに1ラジアン程度変動するので、積分の主要な寄与はこの程度の![]() の値によるのである。
の値によるのである。
![]() をべき級数に展開することもできる。
をべき級数に展開することもできる。![]() の1次の項だけをとればよい。これは、
の1次の項だけをとればよい。これは、![]() の2次までとることを意味する。
の2次までとることを意味する。![]() は
は![]() で置き換えることができる。その誤差は
で置き換えることができる。その誤差は![]() の高次である。左辺を
の高次である。左辺を![]() の1次まで展開し、右辺を
の1次まで展開し、右辺を![]() の1次までおよび
の1次までおよび![]() の2次まで展開すると、
の2次まで展開すると、
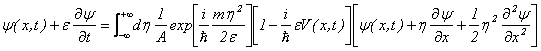
・・・②
が得られる。右辺の主要項をとると、![]() に次の積分を掛けたものが得られる。
に次の積分を掛けたものが得られる。
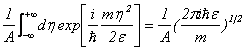 ・・・③
・・・③
左辺の主要項は![]() そのものである。両辺が
そのものである。両辺が![]() の極限で一致するためには③の表式が1となるように
の極限で一致するためには③の表式が1となるように![]() を選ばなければならない。すなわち、
を選ばなければならない。すなわち、
![]()
となる。
②の右辺を評価するために次の2つの積分を使わなければならない。
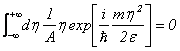
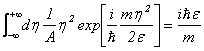
②の右辺を求めると、
![]()
が得られる。もし![]() が次の微分方程式を満たすならば、これは
が次の微分方程式を満たすならば、これは![]() の1次で正しい。
の1次で正しい。
![]()
これは1次元の運動をする粒子の問題に対するシュレディンガー方程式である。
以上は、「ファインマン経路積分と量子力学」(R.P.ファインマン/A.R.ヒッブス著 マグロウヒル)P72~73からの抜粋である。