���ꑊ�ΐ����_�Ɨʎq�����A�����Čo�H�ϕ�
�����I�ȐU���̊p�U������![]() �A�ŗL����
�A�ŗL����![]() �Ƃ���ƁA��H�ɂ�����ϕ��́A
�Ƃ���ƁA��H�ɂ�����ϕ��́A
![]()
�ƂȂ�B
���[�����c�ϊ�
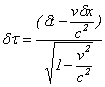
��p����ƁA
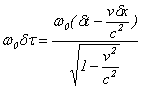
![]()
���A
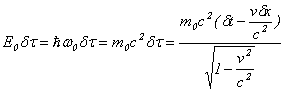
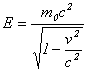 �A
�A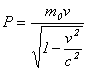
��p����ƁA
![]()
![]()
����́A�{�[�A�̗ʎq�����ł���B
�{�[�A�̗ʎq�����́A�����I�U�������̐��̂�荪���I�Ȃ��̂ł��邱�Ƃ��Ӗ����Ă���B
![]()
�Ə�����Ƃ������Ƃ́A
![]() ��� �@
��� �@
���Ӗ����Ă���A��L�c�_���A
![]() ��� �A
��� �A
![]() ��� �B
��� �B
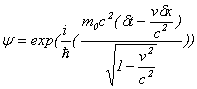 ��� �C
��� �C
�Ƃ����g![]() �̑��݂��Ӗ�����B
�̑��݂��Ӗ�����B
�A�A�B���A��ԂƂ̓��[�����c�ϊ��̌��ʂƂ��ČŗL�����番�h�������̂ƍl�����A�܂��C���A![]() �Ƃ������ʂő�\����镨���́A�g�̈ʑ��̈ʒu�Â��ɍ~�i�����B
�Ƃ������ʂő�\����镨���́A�g�̈ʑ��̈ʒu�Â��ɍ~�i�����B
�u�܂�A��X�͔g���̈ʑ��Ƃ��đ��݂��Ă���̂��B�v�I�I
����́A�h�u���C�ɂ�镨���Ɣg�Ƃ̊֘A�t���̋c�_���A�f�r�b�h�{�[�������W�������l���������A���̐��͇@�Ƃ��������I�ȐU������荪���I�ł��邱�Ƃ�@���ɕ\���Ă���B���ʂ����̔g���̈ʑ��̈ʒu�Â��ɍ~�i����Ă���B
��Ԃ́A�ŗL������̕��h�ɂ������A
�����́A�g���̈ʑ��ɂ����Ȃ��B
����̏����u�̓�q�V���P�v�ɂ��Ɓu�F�v�͋�ԑS�̂������A�u���v�͎��ԑS��(�ߋ��A���݁A����)���Ӗ����A�u�F���v�Ŏ���i���ԂƋ�ԁj�̑S�̂��Ӗ�����B
�܂���p��![]() �Ə����A�B���A
�Ə����A�B���A
![]()
�ƂȂ�A����͌o�H�ϕ��ł悭�o�Ă���`�d�����̂��̂ł���B
��p�ɂ��ĉ����A
![]()
�ƂȂ�B
���ӂ������P��![]() �A����
�A����![]() �A���x
�A���x![]() �Ŋ���ƁA
�Ŋ���ƁA
![]()
�ƂȂ�A����̓G���g���s�[�ł���B�G���g���s�[��![]() �Ƃ���ƁA
�Ƃ���ƁA
![]()
�ł��邩��A
![]()
�܂�A
![]()
�̊W��������B����́A�o�H�ϕ��v�͊w�ɓǂݒ�����@�ŗp�����ϊ����ł���B