波動性からプランクの黒体輻射の公式を導いてみる。

より、

とおくと、

周期的境界条件を課すと、

,　　と定義すると、

ここにlimはｋを連続に持って行く意味。よって、

となります。

同様に、

となりますので、電磁場は、の調和振動子の集まりと同等であります。

次の課題は、調和振動子のエネルギーの期待値

を求めることです。

「よくわかる量子力学（連続性と非連続性とをつなぐ伝播関数）」の中で

という式が出てきましたが、これを三次元に拡張し、伝播関数を

と書いてみます。

物理量の期待値は、

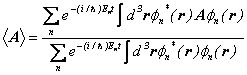
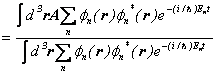
ですので、伝播関数を用いて書き直しますと、

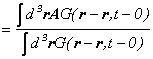
となります。ここで、物理量として、エネルギーを考えてみますと、エネルギーの期待値は、

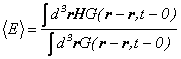
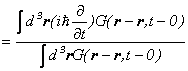　　（　より）

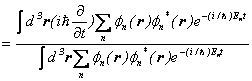
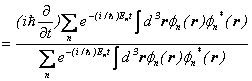
となります。

の式におきまして、

は、モードが２つある調和振動子のエネルギーですので、

　（最初の２は、モードが２つあることを意味しています。）

という量を考えてみますと、

です。を具体的に計算してゆきましょう。

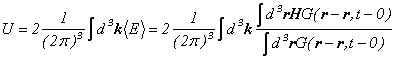
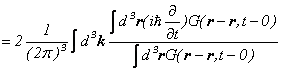
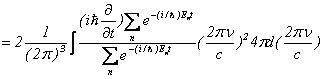
となります。いま、調和振動子のエネルギーを考えていましたので、

と書くことができます。（本当は、　ですが、　は省略します。）

これは、「よくわかる量子力学（連続性と非連続性とをつなぐ伝播関数）」の中で考察しましたように、経路積分によって計算された伝播関数をテーラー展開することによって求めることができます。

従いましては、

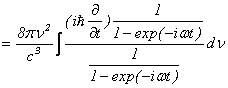
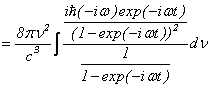
となります。

従いまして、

となります。

経路積分では、時間を虚数にいたしますとウィーナー積分になり、積分が収束しやすくなるという性質があります。そこで、とおき、さらに、とおきますと、

　あるいは、　

となりまして、

となります。

この場合、

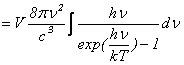
となりまして、プランクの黒体輻射の公式が出てきます。

この議論の中に粒子（光量子）は全く出てきません。

のように、電流のフーリエ変換　　を振幅として持つ波動の変位を一般化座標と見立てて、それをとおいたことにより、電磁場が、の調和振動子の集まりと同等なものとして書き直されただけに過ぎません。

この議論の中で、大切だったのは、エネルギーが、　と飛び飛びになっていることでした。

そして、飛び飛びのエネルギーが出てきたのは、「よくわかる量子力学（連続性と非連続性とをつなぐ伝播関数）」の中で考察しましたように、経路積分によって計算された伝播関数をテーラー展開したからでありまして、なるエネルギー単位を持つ「光量子」が存在するからでは決してありません。伝播関数は作用を位相に持つ指数関数でありましたから、これは波動の性質を持ちます。エネルギーが飛び飛びであることのイメージは、バイオリンの弦が、基準振動の２倍振動、3倍振動、4倍振動･･･という具合の振動のみを許すというものに近いのでありまして、なるエネルギー単位を持つ粒子が1個、2個、3個･･･存在するというものでは全くないのです。電子が光を吸収するという現象は、なるエネルギーを電子が受け取ると、光のバイオリンが例えば3倍振動から2倍振動に遷移する、というものなのです。電子が、なるエネルギー単位を持つ光量子を1個吸収したわけではないのです。（電子もバイオリンの弦のようなものかもしれませんね。）

従いまして、プランクの黒体輻射の公式は、粒子性から導出されたわけではなく、伝播関数という波動性から導出されたのです。

プランクの黒体輻射の公式は、「光量子」の存在を裏付けるものというのが、現代の物理学では常識になっていますが、ここで論じてきましたように、「光量子」などを仮定しなくとも、導出できるものだったのです。

「現代物理のおかしさ」を皮切りにこのホームページを立ち上げました目的の一つが、「光量子」を持ち出さずに、波動性だけからプランクの黒体輻射の公式を導き出すことでした。

以前「現代物理のおかしさ」の中で、以下のような私の姿勢を示しました。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

プランク黒体輻射の公式は実験結果を見事に言い当てていますので、光が電子などとエネルギーのやり取りを行うときには、の整数倍でしかエネルギーのやり取りが出来ないことは、事実として認めてよいでしょう。しかし、この事実を、光が粒子性を持つと解釈したアインシュタインの思考には、かなりの飛躍があるように私には感じられます。光の波を確率の波であるとしてしまい、コペンハーゲン解釈を生み出してしまうといった、現在物理学を間違った方向に導いてしまった分岐点が、まさにこの「光量子」仮説であると私は考えています。

そこで私は、もう一度プランク黒体輻射の公式が発表された直後の時代に立ち戻って、波動性だけで光の本質を説明できないかという課題に取り組んでみました。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

そして、「光量子」を持ち出さずに、波動性だけからプランクの黒体輻射の公式を導き出すことができないかと、この一年間半、考え続けてまいりましたが、ここに、ひとまずの結論が出たものと思っております。

こんな事を考え始めた一年半前、私はファインマンの経路積分などほとんど知りませんでした。しかし思考の過程で必然的にファインマンの経路積分の考え方が必要となり、その理論の中で中心的な役割を果たす伝播関数と、経路積分の中で頻繁に行われる時間を虚時間にするという手法を持ち出すことにより、目的が叶えられたわけです。

時間を虚数にし、その時間をとおく意味につきましては、今後の課題です。

このように置き換えることによって、経路積分の伝播関数

が、統計力学の密度行列

になるというのがポイントです。

「とおき、さらに、とおく」という手法につきましては、

「ファインマン経路積分と量子力学」（R.P.ファインマン／A.R.ヒッブス著　マグロウヒル）の第１０章　統計力学　や

「岩波講座　現代物理学の基礎[第２版]４　量子力学�U」（湯川秀樹／江沢洋／並木美喜雄ほか共著　岩波書店）の第１７章　運動の法則　の　§17.2Green関数、§17.3経路積分（江沢洋　執筆）

のなか等でも言及されておりますことを最後に付け加えておきます。