���ۂ̌����d�g��
���Ȃ��̎���Ɍ���Ă��錻�ۂ́A�u�ŏ���p�̌����v�Ƃ������̂ɏ]���Č���Ă���̂ł��B
�Ⴆ�A�|�e���V����V�̒����^�����Ă��闱�q�̏ꍇ�̃��O�����W���A���i�G�l���M�[�̎��������j�́A
![]()
�ł��̂ŁA�o�H�ϕ��́A
![]()
�Ə����܂��B�����ō�p�́A
![]() �D�D�D�@
�D�D�D�@
�ƂȂ�܂��̂ŁA����͔Ċ��ƌĂ����̂ł��B�Ċ��Ƃ́A����������S�ɓ��肵�����Ɍ��܂�u���v�̂��Ƃł��B�Ⴆ�A����Ȑ�![]() �̉��̖ʐς́A
�̉��̖ʐς́A![]() �ł��̂ŁA���̖ʐς��Ċ��ł��B��
�ł��̂ŁA���̖ʐς��Ċ��ł��B��![]() �����߂Ă�����ƁA�ʐςƂ����u���v�����܂�܂��B��
�����߂Ă�����ƁA�ʐςƂ����u���v�����܂�܂��B��![]() ��ς��Ă�����ƁA����ɉ����Ėʐς��ω����܂��B
��ς��Ă�����ƁA����ɉ����Ėʐς��ω����܂��B
�]���܂��āA�o�H�ϕ��̒��ɏo�Ă���![]() ���C���[�W�Ƃ��Ă͖ʐς̂悤�Ȃ��̂��l���Ă݂�������ƂɂȂ�܂��B��قǂ̖ʐς̗�ł�
���C���[�W�Ƃ��Ă͖ʐς̂悤�Ȃ��̂��l���Ă݂�������ƂɂȂ�܂��B��قǂ̖ʐς̗�ł�![]() �ɑΉ�������̂��A���O�����W���A���i�G�l���M�[�̎��������j
�ɑΉ�������̂��A���O�����W���A���i�G�l���M�[�̎��������j
![]()
�ł��B�@���ɂ��A���̋Ȑ��̉���������![]() ���玞��
���玞��![]() �ɂ킽���Đϕ��������̂�
�ɂ킽���Đϕ��������̂�![]() �ł��̂ŁA
�ł��̂ŁA![]() �͂܂��ɁA���̋Ȑ��̉��̖ʐςƂ������ƂɂȂ�܂��B����ɁA���O�����W���A���͗��q�̂��ǂ�o�H
�͂܂��ɁA���̋Ȑ��̉��̖ʐςƂ������ƂɂȂ�܂��B����ɁA���O�����W���A���͗��q�̂��ǂ�o�H![]() �̊��ł��B�]���܂��āA���q�̂��ǂ�o�H
�̊��ł��B�]���܂��āA���q�̂��ǂ�o�H![]() ����{���߂Ă�����ƁA��p����́u���v�Ɍ��܂�܂��B�o�H��ς��Ă�����A����ɉ����č�p���ω����܂��B
����{���߂Ă�����ƁA��p����́u���v�Ɍ��܂�܂��B�o�H��ς��Ă�����A����ɉ����č�p���ω����܂��B
�_![]() ����_
����_![]() �Ɏ��邠��o�H������߂Ă�����ƁA��p�Ƃ����u���v������܂�܂��B
�Ɏ��邠��o�H������߂Ă�����ƁA��p�Ƃ����u���v������܂�܂��B
�����āA���̍�p���ʑ��i�g���R�ɂȂ��Ă��邩�A�J�ɂȂ��Ă��邩���������l�j�ɂ��g���l���܂��i�o�H�ϕ��̒���![]() �����̔g��\�킵�Ă��܂��B����́A
�����̔g��\�킵�Ă��܂��B����́A![]() �Ƃ������܂��B�j�B�܂�A�o�H������߂Ă�����ƁA����ɑΉ�����g������܂�܂��B�����āA�_
�Ƃ������܂��B�j�B�܂�A�o�H������߂Ă�����ƁA����ɑΉ�����g������܂�܂��B�����āA�_![]() ����_
����_![]() �Ɏ��邠����o�H�ɂ��āA�������č쐬�����g�����ׂđ������킹�܂��B���ꂪ���q���_
�Ɏ��邠����o�H�ɂ��āA�������č쐬�����g�����ׂđ������킹�܂��B���ꂪ���q���_![]() ����_
����_![]() �Ɏ���m���U���ł���Ƃ���̂��A�t�@�C���}���̌o�H�ϕ��ʎq���̍l�����ł��B
�Ɏ���m���U���ł���Ƃ���̂��A�t�@�C���}���̌o�H�ϕ��ʎq���̍l�����ł��B
�o�H�������ω������Ă݂��Ƃ��ɂ́A��p�����Ȃ�ω�����ꍇ������܂����A�܂��قȂ����o�H�̕ω��̂��������������ɂ́A�قƂ�Ǎ�p���ω����Ȃ��Ƃ����ꍇ������܂��B
�܂�A�o�H�������ω������������ł��g�̈ʑ����傫���ω����Ĉʑ������]����i�R�ƒJ���Ђ�����Ԃ�j���Ƃ�����A�o�H�������ω����������ɂ͂قƂ�ǔg�̈ʑ����ω����Ȃ��i�R�͎R�̂܂܁j�Ƃ������Ƃ�����܂��B�o�H��ω������Ă݂��Ƃ��g�̈ʑ����傫���ς���Ă��܂��ꍇ�ɂ́A�����̔g�͎�߂����Ă��܂��A���ʂ��̌o�H�𗱎q�����ǂ�m���͂قƂ�ǂȂ��Ȃ��Ă��܂��܂��B����Ƃ͔��ɁA�o�H�������ω������Ă݂��Ƃ��ɁA�g�̈ʑ����قƂ�Ǖω����Ȃ����́A�����̔g�͋��߂����A���ʂ��̋ߕӂ̌o�H�𗱎q�͂��ǂ邱�ƂɂȂ�܂��B
�g�̈ʑ��͍�p�ł���܂�������A��p���o�H�ɑ��ċɏ��l���Ƃ��Ă��āA�o�H��ω������Ă݂Ă���p���قƂ�Ǖω����Ȃ��o�H���A���ۂɌ���錻�ۂƂ������ƂɂȂ�܂��B
������u�ŏ���p�̌����v�Ɛ\���܂��āA�w�i�̔g�̒�������ۂɂǂ̌��ۂ�����Ă��邩�����߂Ă��鍪�{�I�Ȍ����Ȃ̂ł��B�����Ă��ꂱ�����t�@�C���}���̌o�H�ϕ��ʎq���̐^�����ł���܂��āA�ʎq�_�̈Ӗ����Ă��邱�Ƃ�����ł����B��̗��_�Ȃ̂ł��B
�{�[���𓊂���ƕ������̌o�H��`���܂����A�������ĕ�������`���o�H���������ǂ��Ă���킯�ł͂Ȃ��Ƃ����킯�ł��B�{�[���̓s�b�`���[����L���b�`���[�ւ̂�����o�H�����ǂ��Ă���킯�ł����A���ꂼ��̌o�H�Ɋ��蓖�Ă�ꂽ�g�𑫂����킹�����ʁA��������`���o�H���������ۂƂ��Č���Ă���i�c���Ă���j�ƍl���Ȃ���Ȃ�Ȃ��̂ł��B
��̗ʎq�_�ւ̊g��
����܂ł̋c�_�́A���q���o�H��`���Ĕ��ł䂭�Ƃ��������̂�������邢����u�ʎq�͊w�v�̂��b�ł������A���Ȃǂ��l���鎞�ɂ͓d����ȂǂƂ����悤�Ɂu��̗ʎq�_�v�ɂ��̂��b���g������K�v������܂��B
�������A����قǓ�����b�ł͂���܂���B����ɂ́A���܂܂Ōo�H�Ƃ����Ă������̂���̗ʂɒu�������čl��������̂ł��B�Ⴆ�A�d����̏ꍇ�ɂ́A
�o�H![]() ���x�N�g���|�e���V����
���x�N�g���|�e���V����![]() ��X�J���[�|�e���V����
��X�J���[�|�e���V����![]() �ɒu�������āA
�ɒu�������āA
![]()
�Ƃ����o�H�ϕ����l���Ă݂�����̂ł��B
��قǂ́u�ʎq�͊w�v�̌o�H�̂��b�̒��ł́A�_![]() ����_
����_![]() �Ɏ���o�H�ɂ��čl���܂������A����́u��̗ʎq�_�v�ł́A��̗�
�Ɏ���o�H�ɂ��čl���܂������A����́u��̗ʎq�_�v�ł́A��̗�![]() ��
��![]() ���l���܂��B
���l���܂��B
�Ⴆ�Η��q�Ɠd����̑��ݍ�p���l�����ꍇ�A��p�́A
![]()
![]()
![]()
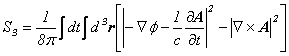
�ƂȂ�܂��B
��قǂ́u�ʎq�͊w�v�̏ꍇ�́A���O�����W���A��
![]()
�̋Ȑ��̉���������![]() ���玞��
���玞��![]() �ɂ킽���Đϕ��������̂�
�ɂ킽���Đϕ��������̂�![]() �ł����̂ŁA
�ł����̂ŁA![]() �́A���̋Ȑ��̉��̖ʐςƂ����C���[�W�ł����B
�́A���̋Ȑ��̉��̖ʐςƂ����C���[�W�ł����B
�����![]() ��
��![]() �ł́A���O�����W���A�����x��
�ł́A���O�����W���A�����x��
![]()
��
![]()
�͎���![]() ��̒��Ȗʂł��̂ŁA��p
��̒��Ȗʂł��̂ŁA��p![]() ��
��![]() �́A���̒��Ȗʂ̉����́u�̐ρv���C���[�W����̂������ł��傤�B
�́A���̒��Ȗʂ̉����́u�̐ρv���C���[�W����̂������ł��傤�B
����![]() �𓌋��h�[���̃O�����h�Ƃ���A
�𓌋��h�[���̃O�����h�Ƃ���A
![]()
��
![]()
�́A�h�[���̖��V��ł��B���̖��V��́A��̗�![]() ��
��![]() �̊��ł��B
�̊��ł��B
�����āA![]() ��
��![]() �́A�h�[���̑̐ρA�h�[����t����\�킵�Ă��܂��B
�́A�h�[���̑̐ρA�h�[����t����\�킵�Ă��܂��B
���V���c��܂�����k�܂����肷��ƁA�h�[���̑̐ς͕ω����܂��B
���V��́A![]() ��
��![]() �̊��ł����̂ŁA��̗ʂ�ω�������ƁA��p���ω����܂��B
�̊��ł����̂ŁA��̗ʂ�ω�������ƁA��p���ω����܂��B
���V��̌`�������߂Ă�����ƁA�����h�[���̑̐ς͈�́u���v�Ɍ��܂�܂��B
�܂�A��̗�![]() ��
��![]() ������߂Ă�����ƁA��p����Ɍ��܂�܂��B
������߂Ă�����ƁA��p����Ɍ��܂�܂��B
�����āA��قǂ́u�ʎq�͊w�v�̎��Ɠ����悤�ɁA���̍�p���ʑ��i�g���R�ɂȂ��Ă��邩�A�J�ɂȂ��Ă��邩���������l�j�ɂ��g���l���܂��B�܂�A��̗ʁi�h�[���̖��V��̌`��j������߂Ă�����ƁA����ɑΉ�����g������܂�܂��B�����āA�������̗ʁi������h�[���̖��V��̌`��j�ɂ��āA�������č쐬�����g�����ׂđ������킹�܂��B���ꂪ���ۂɉ�X���ڂɂ����̊m���U���ł���܂��B
�����h�[���̖��V��̓h�[���̌����̎��͂ɌŒ肳��Ă��܂��̂ŁA��������E�����ɂ��āA�傫���c��܂�����A�k�߂��肷�邱�Ƃ��o���܂����A���V�����������������������Ƃ͏o���܂���B��قǂ́u�ʎq�͊w�v�̎��́A�_![]() �Ɠ_
�Ɠ_![]() ���Œ肵�āA���̊Ԃ̍l����ꂤ��S�Ă̌o�H�ɂ��čl���܂������A�u��̗ʎq�_�v�ł́A���V��̎��͂��Œ肵�A����ɏ�����ԂƏI��Ԃ̖��V��̌`��͌Œ肵����ŁA���̋��E�����̂��ƂŁA�l����ꂤ��S�Ă̖��V��̌`��ɂ��čl���邱�ƂɂȂ�܂��B
���Œ肵�āA���̊Ԃ̍l����ꂤ��S�Ă̌o�H�ɂ��čl���܂������A�u��̗ʎq�_�v�ł́A���V��̎��͂��Œ肵�A����ɏ�����ԂƏI��Ԃ̖��V��̌`��͌Œ肵����ŁA���̋��E�����̂��ƂŁA�l����ꂤ��S�Ă̖��V��̌`��ɂ��čl���邱�ƂɂȂ�܂��B
����![]() �𓌋��h�[���̃O�����h�ɂ��Ƃ��܂����̂ŁA�h�[���̖��V��́A�u����v�̏�ɒ����Ă��開�V��ł��邱�Ƃɒ��ӂ��Ă��������B��Ԃ݂̂̏��ɒ����Ă���Ȗʂł͂Ȃ��A���Ԃ��܂߂��u����v�̏�ɒ����Ă���ȖʂȂ̂Łu���Ȗʁv�ƌ������킯�ł��B
�𓌋��h�[���̃O�����h�ɂ��Ƃ��܂����̂ŁA�h�[���̖��V��́A�u����v�̏�ɒ����Ă��開�V��ł��邱�Ƃɒ��ӂ��Ă��������B��Ԃ݂̂̏��ɒ����Ă���Ȗʂł͂Ȃ��A���Ԃ��܂߂��u����v�̏�ɒ����Ă���ȖʂȂ̂Łu���Ȗʁv�ƌ������킯�ł��B
�h�[���̖��V���1���Ԃ����Ėc��܂�����k�߂��肵�Ă݂܂��傤�B1���Ԃ̊Ԃɂ͒n�������]���܂��̂ŁA�F�����猩��Ɠ����h�[���̈ʒu�������Ă��܂��B�u����v�̕��ʂ̏�����ԕ������ԕ����ɖ��V�䂪�c���k�肵�Ȃ���ړ����Ă���p���C���[�W���Ă݂Ă��������B�ˑR�Ƃ��Ė��V��̎��͂̓h�[���̌����ɌŒ肳��Ă͋���܂����B
�ߌ�7���i������u����P�v�ƌĂт܂��j����ߌ�8���i������u����2�v�ƌĂт܂��j�ɂ����Ė��V���c��܂�����k�܂����肵�܂��ƁA�u����P�v����u����2�v�Ɏ���܂Ŗ��V��͖c���E���k���Ȃ��玞�ʏ���ړ����Ă����܂��B���V��ɂ���ĕ������Ԃ����V��̈ړ��ɂ���āA�����悤�Ɉړ����Ă䂭���ƂɂȂ�A���ʁA�u����P�v����u����2�v�ɂ�����Ԃɖ��V�䂪�����s��������Ԃ̑S�̐ς����܂�܂��B�c���E���k�̎d���ɂ���āA���V��Ƃ���ɂ���ĕ���ꂽ�����̋�Ԃ̑̐ς��قȂ�܂��B�����Ėc���E���k�̎d���Ƃ���ɂ���ĕ�����̐ς͈�Έ�ɑΉ����܂��B�����āA���̑̐ς��ʑ��Ƃ���g���A���ꂼ��̖��V��̖c���E���k�̎d���ɂ��āA�Ή������邱�Ƃ��o���܂��B
���̔g���A�u����P�v����u����2�v�Ɏ��邠���開�V��̖c���E���k�̎d���ɂ��āA�������킹�����ʁA�g�����߂����������������A���ۂƂ��Č���܂��i�c��܂��j�B���ꂪ��X�����ۂɖڂɂ���u��v���邢�́u��̕ϓ��v�ł��B�u����P�v����u����2�v�Ɏ���ɂ������ẮA����u���v�̎��ɁA���V�䂪�ΐ��܂Ŗc���ł���Ƃ����c���E���k�̎d�������邩���m��܂���B���̂Ƃ����ʓI�ɕ���ꂽ��Ԃ̑̐ς͔���ɑ傫�Ȃ��̂ɂȂ�܂��B�܂������u���v�̎��ɁA�n���̃}���g���܂ʼn��ʏ�ɂւ���ł���Ƃ����c���E���k�̎d�������邩���m��܂���B���̂Ƃ������Ȃ�傫�ȑ̐ς����ʓI�ɕ����s�����ɂȂ�܂��B���������c���E���k�̎d�������݂��Ȃ��킯�ł͂Ȃ��̂ł����A�w��̔g�𑫂����킹�����ʁA���̂悤�ȏ�Ԃ͌���ɂ����Ȃ��Ă���A���x�ǂ��Ƃ���Ŗc���E���k���Ă��開�V��݂̂��������͖ڂɂ��邱�ƂɂȂ�܂��B���ꂪ�u��̗ʎq�_�v�ɂ�����u�ŏ���p�̌����v�ŁA���ۂɖڂɂ����i���邢�͏�̕ϓ��j���ǂ̂悤�Ɍ���Ă��邩��\�킷�d�g�݂ł��B
�d����̘b�ɖ߂��܂��ƁA�u�����Ɣ������̑Ώ��łƑΐ����v�ł��b�������܂����悤�ɁA���͎���̒������ʏ�Ɋg����܂��B���������̓����h�[���̖��V��̂��Ƃ��b�̂悤�ɁA���ʏ�Ɋg������i���x�ǂ��Ƃ���Ŗc���E���k�������h�[���̖��V��̕ϓ��ɑ����j���������݂���킯�ł͂Ȃ��̂ł��B�ȉ~��ɍL������i�ꎞ�͉ΐ��܂Ŗc����V��̕ϓ��ɑ����j������A���炰�̂悤�ɂ��ɂႮ�ɂ�Ɗg������i�ꎞ�͒n���̃}���g���܂ʼn��ʏ�ɂւ����V��̕ϓ��ɑ����j�����݂��܂��B
�������A��p![]() ���ʑ��Ƃ���g�̑������킹�̌��ʁA���ʏ�Ɋg����
���ʑ��Ƃ���g�̑������킹�̌��ʁA���ʏ�Ɋg����
�����������ۂƂ��Č���Ă���킯�ł��B
�����ō�p![]() �J�Ɍv�Z���Ă�����ƁA�u����S�ǓI�ϓ_�v�̒��ł��b����
�J�Ɍv�Z���Ă�����ƁA�u����S�ǓI�ϓ_�v�̒��ł��b����
![]()
![]()
�Ƃ�����p���o�Ă��܂��B
���̍�p���g���āA�ŏ���p�̌�����K�p���āA�d����̃G�l���M�[���v�Z���Ă�����ƁA
�u�����Ɣ������̑Ώ��łƑΐ����v�ł��b�����A
![]()
![]()
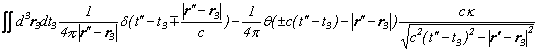
![]()
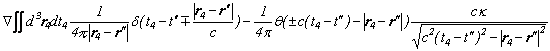
![]()
![]()
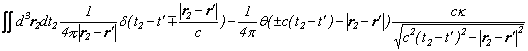
![]()
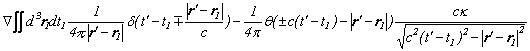
![]()
��A�u�o�H�ϕ��̉^���ʁE�G�l���M�[�\���v�ł��b�����A
![]()
![]()
![]()
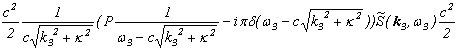
![]()
![]()
![]()
![]()
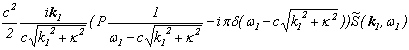
�̎����o�Ă��܂��B�ŏ���p�̌�����K�p�������ʂ������̎��ł��̂ŁA�����̎��������P�Ɂu���ꂽ���ʁv�ɉ߂��Ȃ��̂ł��B�܂�A�����̎��̒��ɂ́A���ʏ�Ɋg����������L�q����Ă��Ȃ��킯�ł��B
�u�o�H�ϕ����E��䶗��v�̒��ł́A���́u���ꂽ���ʁv�ɉ߂��Ȃ��d����̃G�l���M�[�̎��̒��ɂ������A���ԋ�Ԃ̏�ݍ��݂�A���ʗ��̔j��Ȃǂ����Ď�ꂽ���߁A���܂�̋����̂��܂�A�����̎��������E��䶗��Ƒّ��E��䶗��ɑΉ������Ă��܂��܂������A����́A���Ƃ���ł����B�����̎��́A���Ȃ�����̍\�������Ă͂�����̂́A�ǂ�������ꂽ���ۂɉ߂��܂���ł����B���ꂽ���ۂ��A���ԂƋ�Ԃ̐��E�ŕ\�킷���A�^���ʂƃG�l���M�[�̎��ŕ\�킷���̈Ⴂ�ɉ߂��܂���ł����B
�]���܂��āA�����̎��͂ǂ�����ّ��E��������܂���B
�����̎��̔w��ɂ́A����ɁA
![]()
![]()
![]()
![]()
�Ƃ����o�H�ϕ������݂��Ă��邱�Ƃ�Y��Ă͂Ȃ�Ȃ��̂ł��B
�����āA���̌o�H�ϕ������A�S�Ă̑��݂̍����A�����E��䶗��Ȃ̂�������܂���B
����̍l�@�́A����^���@�̑m���̕����璸�����A���[���ł̎�������ƂɁA����܂ł̍l����������x�l�����������̂ł��邱�Ƃ��Ō�ɕt�L�������Ă��������Ǝv���܂��B