経路積分の運動量・エネルギー表示(「物質と反物質の対消滅と対生成」のAppendix)
波動方程式のグリーン関数は、以下のような性質があります。
![]()
![]()
![]()
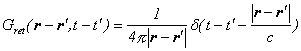
![]()
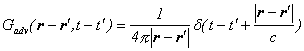
![]()
このグリーン関数を用いて、ベクトルポテンシャルの満たす波動方程式を解きます。
![]()
![]()
すると、電磁場のエネルギーは
![]()
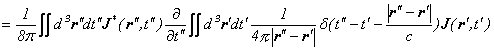
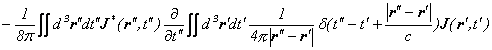
となります。
「物質と反物質の対消滅と対生成」で、電磁場のエネルギーの式は、フーリエ変換前の時間と空間の世界では、以下のような美しい式になっていることを見ました。
![]()
![]()

![]()
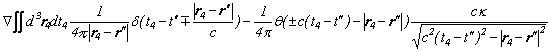
![]()
![]()
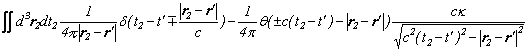
![]()
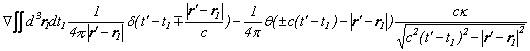
![]()
そこで今回は、この式にフーリエ変換を施してみて、運動量・エネルギーの世界では電磁場のエネルギーがどのように表わされるかを見てみましょう。
源泉の電流は、
![]()
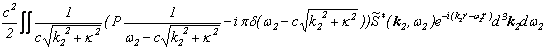
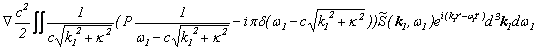
でありますので(「ファインマンの経路積分の畳み込み積における対称性」を参照)、これをフーリエ変換すると、それぞれをフーリエ変換したものの畳み込み積の形になります。
![]()
![]()
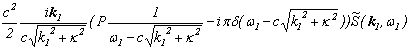
光子の伝播部分は、
![]()
![]()
ですので、これの時間微分は、
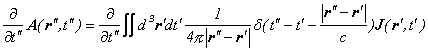
![]()
となります。
観測装置側の電流は、
![]()
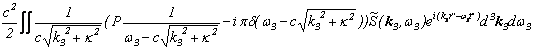
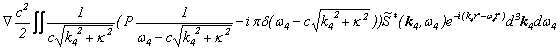
でありますので、先ほどと同様に、フーリエ変換を行うと、
![]()
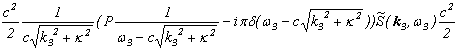
![]()
となります。
従いまして、観測装置側の電流とベクトルポテンシャルの時間微分との積のフーリエ変換は、
![]()
上記のように、それぞれをフーリエ変換したものの畳み込み積になります。
![]()
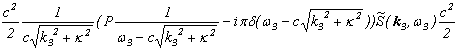
![]()
ですので、
電磁場のエネルギーの式
![]()
に相当いたしますものは、結果的に以下のように表わすことが出来ます。
![]()
![]()
![]()
![]()
![]()
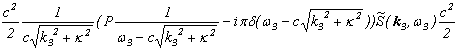
![]()
![]()
![]()
![]()
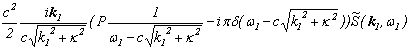
(ここで、![]()
![]() 等のフーリエ変換の際に出てくる係数は省いています。)
等のフーリエ変換の際に出てくる係数は省いています。)

運動量とエネルギーが![]() の相対論的粒子が、運動量とエネルギーが
の相対論的粒子が、運動量とエネルギーが![]() の光子を放出して、運動量とエネルギーが
の光子を放出して、運動量とエネルギーが![]() に減ります。
に減ります。
運動量とエネルギーが![]() の相対論的粒子が、運動量とエネルギーが
の相対論的粒子が、運動量とエネルギーが![]() の光子を吸収して、運動量とエネルギーが
の光子を吸収して、運動量とエネルギーが![]() に増えます。
に増えます。
この電磁場のエネルギーの式やそれを図にしたファインマンダイアグラムはこのようなことを表現しています。
つまり、運動量保存則とエネルギー保存則が、この式では表現されているわけです。
「物質と反物質の対消滅と対生成」で見た時間と空間の世界の式では、時間を逆行したりする粒子が出てきたり、その粒子も実は粒子ではなく球面状に拡がる波であったり、時間や空間の畳み込みがあったりして、この世界が実はとても不思議な作りになっていることが見てとれました。
この不思議な式をフーリエ変換すると、単なる運動量保存とエネルギー保存の式になってしまうわけです(この法則は古典物理学でもおなじみの法則です)。
言い換えれば、現象として現れている、運動量保存則やエネルギー保存則の背後には、時間空間世界における因果律の破れや粒子の波動性、時間と空間の畳み込みなどという性質が、その仕組みとして裏側に隠れていることが分かったわけです。
「運動量・エネルギーの世界」と、「時間・空間の世界」とは、表裏一体の対を成す構造になっているのです。
この運動量・エネルギーの世界で表わされた電磁場のエネルギーの式も、「物質と反物質の対消滅と対生成」で見た時間と空間の世界の式と同じように、大変シンプルで美しい式になっていることが見てとれます。
時間と空間の世界で表わされた式が、グリーン関数やベッセル関数などの複雑な特殊関数で表わされていたことに比べまして、こちらの運動量・エネルギーの世界で表わされた式は、簡単な分数関数であらわされていることが分かります。
これが、通常場の量子論でファインマンダイアグラムを描くときには、フーリエ変換後の運動量とエネルギーの表記で計算ということの理由です。
現代物理の素粒子論では、ファインマンダイアグラムからファインマン規則に従って、様々な量を高い精度で計算することが出来ますが、このような規則を作り出すことが出来たのは、
① 時間空間側のグリーン関数(伝播関数)をフーリエ変換すると、運動量・エネルギー空間側では、簡単な分数関数になること。
② 時間空間側ではグリーン関数(伝播関数)の畳み込み積になっていますが、フーリエ変換すると、運動量・エネルギー空間側では、分数関数の掛け算に基本的になること。
が、大きな理由なのです。
さらに、この式は、相対論的粒子と光子とのビリヤード、つまりコンプトン効果が表現されています。上記の議論の中では、電磁場の波動方程式と、相対論的粒子場のKlein-Gordon方程式のみしか使用しておりません。つまり粒子性を用いることなく、波動性のみからコンプトン効果の運動量保存則やエネルギー保存則を導き出せたわけです。現在、コンプトン効果は光の粒子性の証明であるとされていますが、上記の議論では、光の粒子性など持ち出さずとも、波動方程式だけでコンプトン効果の運動量保存則やエネルギー保存則を導き出せたわけですから、「コンプトン効果は光の粒子性の証明である」という結論には、かなりの飛躍があるように思っております。
そして、この運動量保存則やエネルギー保存則は、上記議論の式変形の過程を追ってみればわかるように、フーリエ変換における畳み込み積の結果として、運動量保存則やエネルギー保存則が説明できるという大変興味深い事実にも気が付きます。
運動量保存則やエネルギー保存則は天下り的に与えられたものでしたが、この世を波動と考えることによって、これらは、「天下り的に与えるもの」ではなく、波動性から「導き出せるもの」になったわけです。