光の2重スリットの実験に関する若干大胆な考察

一般に光源から出た光は360度の全方向に放射されますが、光学機器や目で観測するということは、この全方向に放射された光のごく一部（ごく小さな立体角）を見ることに他なりません。

つまり「観測する」ということは、「観測装置と光源との方向が決まる」という事であります。瞳孔と星などを想像してみれば良いでしょう。

観測する前は、

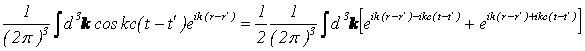
のような任意のをもつ平面波の重ね合わせであったものが、観測という行為で、観測装置と光源との方向が決まったことにより、

のような、包絡線がデルタ関数で群速度がｃの波束が現れる事を「光の波動性と粒子性、及び波束の収縮についての考察」で述べました。これは、1つの光源から出た光をそのまま網膜で受ける、といった時のイメージです。

さて、2重スリットの実験のように光源（スリットの穴）が2つ有る場合を考えて見ましょう。

観測者の位置を、スリット1の位置を、スリット2の位置をとしますと、

観測する前は、

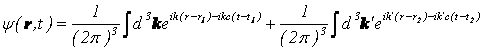
という波の振幅が存在します（ここでは遅延波のみを扱います）。

よって、

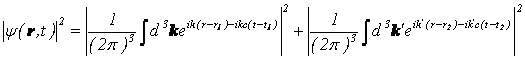
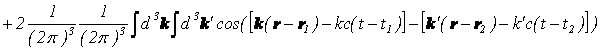
となり、

コサインの項が出てきましたので、位置によって波の強度が異なり、つまり干渉縞が存在することが分かります。

観測する前には確かに干渉縞が存在します。

観測前にこのような状態で存在していた波を、では実際に観測してみましょう。

スリットから出た光を観測する（「観測装置と光源との方向を決める」）ことにより、観測者の場所には、時刻において、

という波の振幅が観測されます。

ここで、はスリット1から見た観測者の方向を、はスリット2から見た観測者の方向をそれぞれ表わします。

これは、「光の波動性と粒子性、及び波束の収縮についての考察」で述べたことを、2つの光源がある場合に拡張しただけのことです。

よって、

さらに、と、とはそれぞれ平行であり、波数がの単色光を仮定すると、

でありますので、

となり、

やはり、コサインの項が出てきてしまいましたが、今回は、観測前の状況とは若干異なります。

デルタ関数があるために、コサインの中身は必ず0（つまりコサインの値は1）になるからです。

この為、最終的には、

となり、干渉縞が消えてしまいました！（つまり、2重スリットの実験における波束の収縮！）。

そして同時に、コサインの値が常に1となっている為、2重スリットから出てきた光を観測する際には、位置によらず、常に一定の強度で、光が観測されることを、この事実は暗示しています。これは、観測される時の光子は、常に1個で観測され、半分の光子や1/4の光子などで観測されることは決してないという、2重スリットの実験結果をうまく説明しています。

つまり、波動性だけでも、2重スリットの実験結果をかなりうまく説明できそうなのです。

が、数学的な問題があることをここで認めなければなりません。

それは、などと、平然と書きましたが、のような特異点の重なる特殊関数の積は、超関数論では実は厳密には定義されていないのです。

このようなものが出てきてしまったのは、波を「線形理論」の枠組みの中だけで考えているからの様な気もします。

あるいは、この問題は、ニュートンが導入した微分積分の概念や、ディラックが導入したデルタ関数の概念のように、物理学側が、道具精神を発揮して、解決するべきものかもしれません。もしも良い方法や道具が見つかれば、数学的基礎付けは、おそらく数学者がこれまでのようにやってくれることでしょう。

従いまして、どちらに致しましても、ここで述べた議論は、物理学会などでは到底受け入れられるものではありません。

が、ここでの議論は、趣味として物理を楽しむ上では、とてもエレガントな数式展開になっています。

既存の物理学は、既存の数学を使って、慎重にこの世界を近似するモデルを作ることに傾注してきました。しかしこの慎重さが逆にあだになって、自然の本来の姿を歪めてしまう様なモデルを作ってしまうこともあったかもしれません。

ですので、自然の本来の姿に近づくためには、少しこの慎重さを捨てて、大胆に考察することも大切なのかも知れません。