相対論的粒子の波動性と粒子性、及び波束の収縮についての考察（諸行無常と相対論的粒子場のAppendix）

Klein-Gordon方程式のグリーン関数は、以下を満たす。

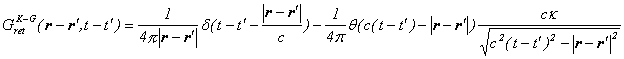
　　　J₁は１次のBessel関数。

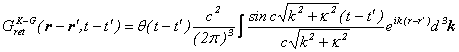
このグリーン関数を用いて、相対論的粒子場の満たすKlein-Gordon方程式を解く。

　　

　　　　

　　　　

　　　　

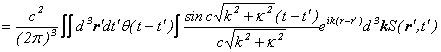
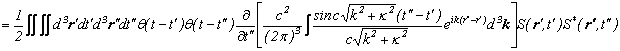
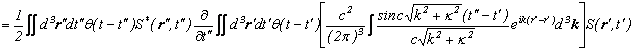
さて、

であり、これは平面波を表している。

ここで、「観測する」という事が物理的に何を表しているのかを考えてみる。一般に源泉から出た波は360度の全方向に放射されるが、観測するということは、この全方向に放射された波のごく一部（ごく小さな立体角）を観測することに他ならない。

つまり「観測する」ということは、「観測装置と源泉との方向が決まる」という事である。

そこで、波数ベクトルkを、観測によって決まったk₀でテーラー展開する。

　

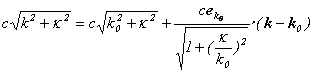
よって、

となるので、平面波は、

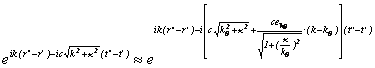
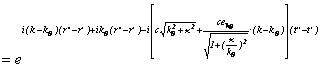
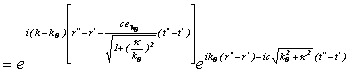
と近似できる。よって、

　　　

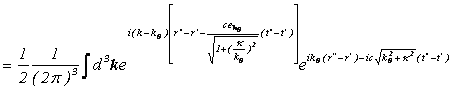
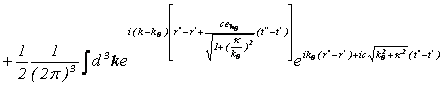
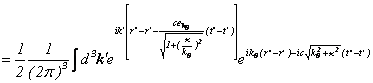
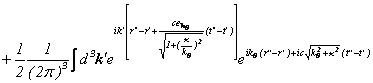
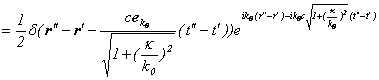
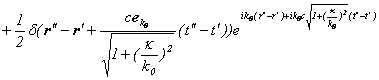
となり、テーラー展開により、包絡線がデルタ関数で群速度が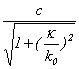、位相速度がの波束が現れた。

よって、相対論的粒子場のエネルギーは、

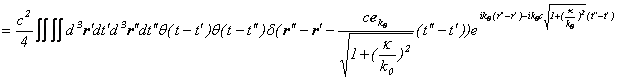
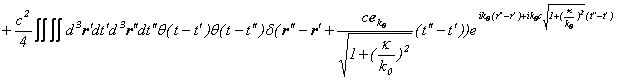
となる。

この式は、振幅がS（源泉）で、包絡線がデルタ関数、群速度が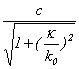、位相速度がの波束が、別のS（観測装置）と相互作用しているという描像を表している。

そして、この波束が、場から顕現した相対論的粒子である。

相対論的粒子は質量があるため、位相速度が波数の関数となり分散性波動の性質を示す。

よって、相対論的粒子場から顕現した波束は、電磁場から顕現した波束とは異なり、時間の経過とともに波束の形状は崩れ、粒子性が永続することはない。