光の波動性と粒子性、及び波束の収縮についての考察（現代物理のおかしさのAppendix）

三次元波動方程式のグリーン関数は、以下を満たします。

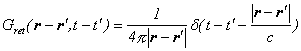
このグリーン関数を用いて、ベクトルポテンシャルの満たす波動方程式を解きます。

　　

　　

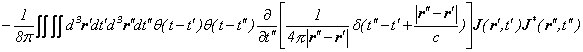
最後の式は、源泉（光源の電流分布）が、三次元波動方程式のグリーン関数（攪乱が尾を引かない球面波）で伝播し、伝播後の波を時間微分したもの（これはEすなわち電場であります）が、もう一度電流分布と相互作用しているという描像を表しています。

さて、

であり、これは平面波を表しています。

ここで、「観測する」という事が物理的に何を表しているのかを考えてみます。一般に光源から出た光は360度の全方向に放射されますが、光学機器や目で観測するということは、この全方向に放射された光のごく一部（ごく小さな立体角）を見ることに他なりません。

つまり「観測する」ということは、「観測装置と光源との方向が決まる」という事であります。瞳孔と星などを想像してみれば良いでしょう。

そこで、波数ベクトルkを、観測によって決まったk₀でテーラー展開してみます。

　

　　　　　

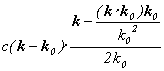
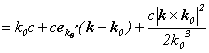
さらにkの2次以上の項を無視すると、

となりますので、平面波は、

と近似できます。よって、

　　　

となり、テーラー展開により、包絡線がデルタ関数で群速度がｃの波束が現れました。

よって、電磁場のエネルギーは、

となります。

この式は、振幅が光源の電流分布ベクトルで、包絡線がデルタ関数、群速度がｃの波束（これはEすなわち電場である！）が、電流分布と相互作用しているという描像を表しています。

テーラー展開（つまり観測）前後の式を比較してみると大変興味深いです。

球面波の時間微分で表される電場の波（これは平面波である）が、観測することによって、包絡線がデルタ関数の波束に変化した（つまり収縮した）と読めます。

またこのことは、左側の電流分布を観測装置と考えれば、観測装置が撃力的な電場で「叩かれる」というイメージがよくあてはまります。

よって光の粒子性は、撃力的な電場が「生ずる」事に帰着できるのでありまして、エネルギー粒子が存在するのではないと考えています。

光源からは電場がおだやかな「波」として伝播し、観測装置と相互作用する瞬間に電場が撃力に変化する、これが光の波動性と粒子性としてこれまで言われてきたことの実態であると結論できるのではないでしょうか。

コペンハーゲン解釈では、確率波としての波が、観測することによって、光子という実態に、波束の収縮を起こすという解釈になっていますが、この収縮のメカニズムは解明されておりません。

今回の考察では、観測前の波は確率波ではなく、光の波そのもの（実態）であります。観測することにより、光子が発生するわけではなく、そこに撃力が発生するのであります。この撃力こそが光電効果やコンプトン効果を引き起こす原因となっていると考えてもいいのではないでしょうか。

そして、波束の収縮のメカニズムは、「波数ベクトルのテーラー展開を行う」事に他ならないのです。