�A�����Ɣ�A�����͑�������T�O�ł͂Ȃ��B�i���Ԃ̗�����Ɋւ����l�@�j
����܂ł̋c�_�ł��т��яo�Ă����A
![]()
�ɂ��āA�l���Ă݂܂��傤�B
����́A�I�C���[�̌����ɂ��A
![]()
�Ə����A�܂��ɔg�̊�{�I�Ȏ��ŁA�A�����̑�\�ł��B
����A�A�C���V���^�C���|�h�u���C�̌���![]() ���A
���A
![]() ����@
����@
�ł����A�V�����f�B���K�[������
![]()
���A�G�l���M�[![]() �̃n�~���g�j�A��
�̃n�~���g�j�A��![]() ��
��
�`���I�ɁA
![]()
�Ə����܂��B������A�@�ɑ�����Ă݂�ƁA![]() �́A
�́A
![]() ����A
����A
�Ƃ����A���Z�q�ɑΉ����邱�Ƃ�������܂��i����́A���Ԃ�i�߂鎞�Ԕ��W���Z�q�ł��B�V�����f�B���K�[���������`���I�ɉ����ƁA![]() �ƂȂ�܂��̂ŁA��Ԃ�������Ԃ���A
�ƂȂ�܂��̂ŁA��Ԃ�������Ԃ���A![]() �����i�߂���������Ă��邱�Ƃ�������܂��B�j�B
�����i�߂���������Ă��邱�Ƃ�������܂��B�j�B
![]()
�ł��̂ŁA���������̊��ɂ�������Z������Ƃ������Ƃ��l������ƁA
![]()
![]()
![]()
![]() �i
�i![]() �̃N���X�̍��j
�̃N���X�̍��j
![]()
![]()
�ƂȂ�A�A�����̑�\�̔g�ł�����![]() �́A
�́A![]() �Ƃ������Z�q�̘a��
�Ƃ������Z�q�̘a��![]() �̘a�ɗ��U���i��A�����j����܂��B
�̘a�ɗ��U���i��A�����j����܂��B
�܂�A���̉F���́A�A���̒������A���̊T�O���������Ă�����ɂȂ��Ă���l�ł��B
������V�����f�B���K�[�������̌`����
![]()
�ɗp����ƁA
![]()
�ƂȂ�܂��B��Q���́A![]() �̃e�[���[�W�J�̌`�����Ă���܂��̂ŁA���Ԃ�
�̃e�[���[�W�J�̌`�����Ă���܂��̂ŁA���Ԃ�![]() �����ψʂ����Ă���Ƃ����������ĂƂ�܂��B
�����ψʂ����Ă���Ƃ����������ĂƂ�܂��B
���݂̗ʎq�͊w�ł͎��Ԃ̓p�����[�^�ł���܂��āA�ǂ�ȏ��ł������W�X�Ɨ����
���̂ł����A�����ŁA���_�ȉ�������Ă݂܂��傤�B
�u�j���[�g���͊w�͔g�����̋A���v�̂Ƃ���ŁA���g��������Ȃ�������ɋ߂Â��Ă䂭�ƁA���Ԃ̌o�߂͌���Ȃ��O�ɋߕt���čs���A�Ƃ����b�����܂����̂ŁA���g���̑召�ɂ���Ď��Ԃ̗��ꂪ�قȂ�ƍl���Ă݂܂��B
���g���A�܂�G�l���M�[���傫���Ȃ�Ǝ��Ԃ̗��ꂪ�ɖ��ɂȂ�܂��̂ŁA���ԕ����̌X�����������Ȃ�Ƃ�����_�ȉ�������Ă݂܂��B�����Ă��̌X�����A�{���c�}�����z�ɔ�Ⴗ��Ɖ��肵�Ă݂܂��B�܂�A
![]()
�Ƃ��Ă݂܂��B����ƇA�͂���ɁA
![]()
�Ƃ������Z�q�ɂȂ�܂��B
![]()
�ł��̂ŁA���������̊��ɂ�������Z������Ƃ������Ƃ��l������ƁA
![]()
![]()
![]()
![]() �i
�i![]() �̃N���X�̍��j
�̃N���X�̍��j
![]()
![]()
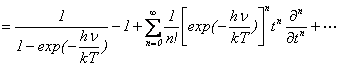
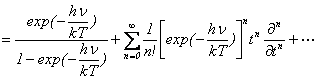
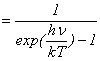 �i����́A�v�����N�̍����t�˂̌����ŁA���ϗʎq����\�킵�܂��B�j
�i����́A�v�����N�̍����t�˂̌����ŁA���ϗʎq����\�킵�܂��B�j
![]()
�ƂȂ�A�A�����̑�\�̔g�ł�����![]() �́A
�́A![]() �Ƃ����ʎq�����ꂽ�{���c�}�����z�̊m���A�̘a��A
�Ƃ����ʎq�����ꂽ�{���c�}�����z�̊m���A�̘a��A![]() �̘a�Ȃǂɗ��U���i��A�����j����܂��B
�̘a�Ȃǂɗ��U���i��A�����j����܂��B
������V�����f�B���K�[�������̌`����
![]()
�ɗp����ƁA
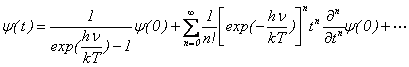
�ƂȂ�܂��B��Q���́A���g���ɉ����āA���Ԃ�![]() �����ψʂ��Ă���Ƃ����������ĂƂ�܂��B
�����ψʂ��Ă���Ƃ����������ĂƂ�܂��B
�V�����f�B���K�[�������̌`����
![]()
�ɂ����āA
![]()
�́A���Ԃ�i�߂鎖���Ӗ����鎞�Ԕ��W���Z�q�ł��̂ŁA
![]()
���A���g���ɂ�炸���Ԃ̐i�ݕ��͓����Ƃ����`�����Ƃ���ƁA
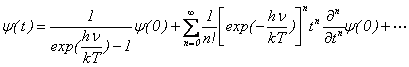
�́A���g���ɂ���Ď��Ԃ̐i�ݕ����قȂ�Ƃ����`����\�킵�Ă���ƍl���邱�Ƃ��o����̂ł͂Ȃ��ł��傤���B
�����āA���̕`�����A�ÓT�͊w�i�A���I�Ȑ��E�j����ʎq�͊w�i��A���I�Ȑ��E�j�Ɉڍs����ۂɌ��ꂽ�A�v�����N�̍����t�˂̌����Ɨގ����Ă���iAppendix�Q�Ɓj���́A���ɋ����[�������ł��B
�ÓT�_�ł́A�G�l���M�[�����z�����烌�C���[�W�[���Y�̌������o�Ă��܂������A�ʎq�_�ł́A�G�l���M�[�����z�������藧�����A�v�����N�̌����ɂȂ邱�Ƃ�������܂����B
���̗ސ��ő�_�ɍl����A���Ԃ������z����Ă��Ȃ��̂�������܂���B
����܂ŁA������q�ׂĂ����悤�ɁA��ԂƉ^���ʂ̓t�[���G�ϊ��Ō���Ă������ŁA���ԂƃG�l���M�[���t�[���G�ϊ��Ō���Ă��܂��B
�t�[���G�ϊ��Ō���Ă���̂ŁA![]() �A
�A![]() �Ƃ����s�m�萫�W�����藧���܂��B
�Ƃ����s�m�萫�W�����藧���܂��B
�A�C���V���^�C���̌��ʎq�_�ŃG�l���M�[���ʎq������Ă���Ƃ���A���Ԃ��ʎq������Ă���ƍl������̂ł͂Ȃ��ł��傤���B�����āA���Ԃ̗ʎq�_�H�ł́A�ʎq�����ꂽ���Ԃ̓����z�������藧�����A���̌��ʁA�ʎq�����ꂽ�G�l���M�[���傫���Ȃ�ɂ��������āA�ʎq�����ꂽ���Ԃ̐i��͏������Ȃ�̂ł͂Ȃ��ł��傤���B
���ہA���g���i�G�l���M�[�j���傫���Ȃ�Ȃ�ق�![]() �͑傫���Ȃ�A�G�l���M�[�Ǝ��Ԃ̕s�m�萫�W����
�͑傫���Ȃ�A�G�l���M�[�Ǝ��Ԃ̕s�m�萫�W����![]() �͏������Ȃ�͂��ł��B
�͏������Ȃ�͂��ł��B
��ԂƉ^���ʂɑΏ̐�������悤�ɁA���ԂƃG�l���M�[�ɂ��Ă��Ώ̐������݂���͂��Ȃ̂ł��B
Appendix
�{���c�}�����z���ɂ��ƁA���x![]() �̕��t��Ԃɂ����ăG�l���M�[
�̕��t��Ԃɂ����ăG�l���M�[![]() �̏�Ԃɂ���m����
�̏�Ԃɂ���m����![]() �ɔ�Ⴕ�܂��B
�ɔ�Ⴕ�܂��B
���̂Ƃ��G�l���M�[���A���ʂł���Ƃ���ƁA�n�̃G�l���M�[�̕��ϒl��
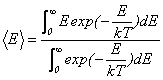
�Ə����܂��B�E�ӂ̕��q���ϕ�����A
![]()
![]()
���A
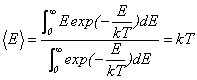
�ƂȂ�܂��i���ꂪ�A�G�l���M�[�����z���j�B
����āA�����t�˂̃X�y�N�g�����z�́A�ÓT�_�ɂ��ƁA
![]()
�ƂȂ�܂��i���C���[�W�[���Y�̌����j�B
����A�ʎq�_�ł́A�G�l���M�[�͘A���ʂł͂Ȃ��A![]() �̐����{�̒l�����Ƃ�Ȃ��ƍl���܂��i�A�C���V���^�C���̌��ʎq�_�j�B����ƁA�n�̃G�l���M�[�̕��ϒl�́A�ϕ��ł͂Ȃ��a�ƂȂ�܂��̂ŁA
�̐����{�̒l�����Ƃ�Ȃ��ƍl���܂��i�A�C���V���^�C���̌��ʎq�_�j�B����ƁA�n�̃G�l���M�[�̕��ϒl�́A�ϕ��ł͂Ȃ��a�ƂȂ�܂��̂ŁA
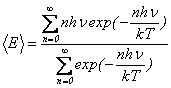
�ƂȂ�܂��B
���q�́A
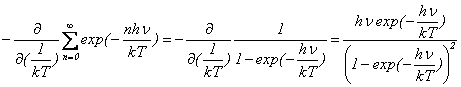
����́A
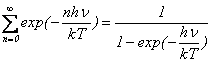
�Ȃ̂ŁA
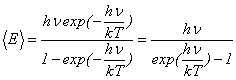
�ƂȂ�܂��i�U�����ɂ���Ĕz����G�l���M�[���قȂ��Ă���A�G�l���M�[�����z�������藧���Ă��Ȃ��j�B
�����āA�����t�˂̃X�y�N�g�����z�́A�ʎq�_�ɂ��ƁA
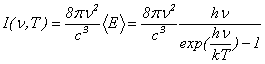
�ƂȂ�܂��i�v�����N�̌����j�B