�t�@�C���}���̌o�H�ϕ��̏�ݍ��ݐςɂ�����Ώ̐�
�t�@�C���}���̌o�H�ϕ��ʎq���̕��@�ł́A�����̏ꏊ�̏�Ԋ��́A������Ɠ`�d���̏�ݍ��ݐςŕ\�킷���Ƃ��o���܂��B
![]() ����@
����@
![]() ��
��![]() �����ꂼ��t�[���G�ϊ��ŕ\�킷�ƁA
�����ꂼ��t�[���G�ϊ��ŕ\�킷�ƁA
![]() ����A
����A
![]() ����B
����B
�G�l���M�[�E�^���ʋ�ԑ��̏�Ԋ��́A�B�̃t�[���G�t�ϊ��ŕ\�킹��̂ŁA
![]()
�@��������ƁA
![]()
�X�ɇA��������ƁA
![]()
![]()
![]()
�����ɁA
![]()
�ƒu�����B
�܂�A����ԑ��ł́A
![]()
�̂悤�ɁA�����̏ꏊ�̏�Ԋ��́A������Ɠ`�d���̏�ݍ��ݐςŕ\�킷���Ƃ��o���܂��i�����̏ꏊ�̏�Ԃɂ́A�����鎞���A�������Ԃ̏�Ԃ��`�d���ɂ���ĉ^���ݍ��܂�Ă��܂��j���A�G�l���M�[�E�^���ʋ�ԑ��̓`�d�����A
![]()
�ƒu�����Ƃɂ��A�G�l���M�[�E�^���ʋ�ԑ��̏�Ԋ����A
![]()
�Ƃ����l�ɁA�G�l���M�[�E�^���ʋ�ԑ��̌�����ƃG�l���M�[�E�^���ʋ�ԑ��̓`�d���̏�ݍ��ݐςŕ\�킷���Ƃ��o���܂��i����G�l���M�[����^���ʂŕ\�킹���Ԃɂ́A������G�l���M�[�A������^���ʂ̏�Ԃ��G�l���M�[�E�^���ʋ�Ԃ̓`�d���ɂ���ĉ^���ݍ��܂�Ă��܂��j�B
����āA
![]()
![]()
���邢�́A
![]()
![]()
�ƂȂ�܂��B
�t�@�C���}���̌o�H�ϕ��ł́A
���ԂƋ�Ԃ̐��E�ƁA�G�l���M�[�i�U�����j�Ɖ^���ʁi�g���j�̐��E�Ƃ��A�����ȃV�����g���[�ɂȂ��Ă��邱�Ƃ�������܂��B
�G�l���M�[�Ɖ^���ʂ̐��E�ɂ����āA
���̉^���ʂɁA������^���ʂ���ݍ��܂�Ă��܂��B
�����āA���̃G�l���M�[�ɂ́A������G�l���M�[����ݍ��܂�Ă��܂��B
���ԂƋ�Ԃ̐��E�ɂ����āA
���̈�_�ɁA������F������ݍ��܂�Ă��܂��B
�����āA���̈�u�ɁA�ߋ��A���݁A��������ݍ��܂�Ă���̂ł��B
�Ⴆ�A���i�x�N�g���|�e���V�����j�̏ꍇ�A���ԋ�Ԃ̐��E�ł̏�ݍ��݂́A
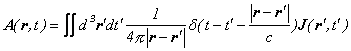 �����
�����
�ƕ\�킹�A����ŁA
![]()
![]()
![]() �����
�����
�ł���̂ŁiAppendix�Q�Ɓj�A�G�l���M�[�E�^���ʂ̐��E�ł̏�ݍ��݂́A
![]()
![]() �����
�����
�ƂȂ�܂��B
�����āA�����́u���ԋ�Ԃ̐��E���v�Ɓu�G�l���M�[�E�^���ʂ̐��E���v�́A���̃t�[���G�ϊ��ł��݂��Ɍ��т��Ă��܂��B
Appendix�i�t�@�C���}���̌o�H�ϕ����猩���`�����g�����x�N�g���|�e���V�����A�d��A����̌v�Z�j
![]()
![]()
![]()
![]()
![]()
![]()
![]()
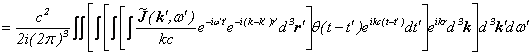
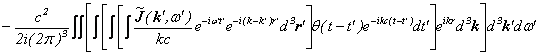
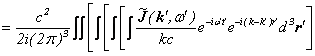
![]()

![]()
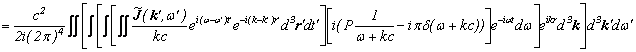
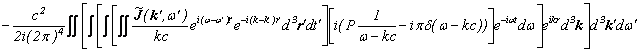
![]()
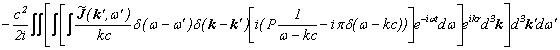
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()