光のエネルギーの様々な描像

（１）光源から球面波状に広がった光の波が観測装置と相互作用するという描像（既出）

（２）光源と観測装置が局在している場合、光子という粒子性が現れるという描像（既出）

（３）波動性からプランクの黒体輻射の公式を導いてみる。

より、

とおくと、

周期的境界条件を課すと、

,　　と定義すると、

ここにlimはｋを連続に持って行く意味。よって、

　　（ボーアの量子条件を使用）

（４）ファインマンの経路積分から見た描像

よって、

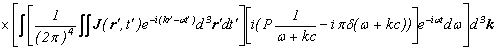
ここで、

は、光源のフーリエ変換であり、

は、伝播関数のフーリエ変換に関係するものであります。

ベクトルポテンシャルＡは、光源と伝播関数の畳み込み積の形で表わされていたため、ベクトルポテンシャルをフーリエ変換すると、それは、光源のフーリエ変換と伝播関数のフーリエ変換のそれぞれの積で表わすことが出来ます。これは、ファインマンの経路積分の確率振幅の考え方に対応しております。

場の量子論（第二量子化）では、周期的境界条件を課してベクトルポテンシャルを平面波でフーリエ級数展開する、という手法をとりますが、これはかなり無理のある特異な手法であると私は感じております。場の量子論では、この手法を用いて、場を調和振動子の集まりに持って行き、生成消滅演算子を導出して、理論を展開しますが、場の量子論における生成消滅演算子の考え方は、このファインマンの経路積分から見た描像を簡略化した近似であると考えております。

この描像に現れる、

は、時間と共にデルタ関数に近付いてくるものですので、これが生成消滅演算子と密接にかかわっている量であると私は考えております。