�j���[�g���͊w�͔g�����̋A��
�ȑO�u�B���I���R�Ȋw�ς̔ے�v�ŁA���̐��E���g�������炱���A�n�C�[���x���O�̕s�m�萫���������藧�Ƃ������b�����܂����B
���낢��ȉ^���ʁi���x�Ƃ����Ă��悢�j�̔g�������Ă䂭�ƁA�ʒu���͂�����Ƃ����V���[�v�Ȕg���o���܂��B
��̉^���ʂ̔g�́A�S��ԂɊg�����Ă��܂��܂��B
���ꂪ�A�ʒu�Ƒ��x���ɐ��m�ɑ���ł��Ȃ��s�m�萫�����̐��̂ŁA�g���i�g�̂����܂�j�̐����Ƃ��Đ������o���܂��B
�����āA�s�m�萫���������藧����A�j���[�g���̉^�������������藧�̂��Ǝ��͍ŋߍl���Ă��܂��B
�ʒu�Ɖ^���ʂ̕s�m�萫�W�́A
![]() ����@
����@
�����ŁA![]() �͈ʒu�̕s�m�肳�A
�͈ʒu�̕s�m�肳�A![]() �͉^���ʂ̕s�m�肳�A
�͉^���ʂ̕s�m�肳�A![]() �̓v�����N�萔�ł��B
�̓v�����N�萔�ł��B
�܂��A�G�l���M�[�Ǝ��Ԃɂ��Ă����l�ɕs�m�萫�W�����藧���܂��B
![]() ����A
����A
�@�A�A���A
![]() ����B
����B
�����藧���܂����A�}�N���Ȏړx�i�j���[�g���I���E�j�ʼn^���ʂ��ω�����ꍇ�A�@���ʒu�̕ω��͔����Ȃ��̂ƂȂ�܂��B���l�Ƀ}�N���Ȏړx�ŃG�l���M�[���ω�����ꍇ�A�A��莞�Ԃ̕ω��͔����Ȃ��̂ɂȂ�܂��B����āA�}�N���Ȏړx�ōl����ƇB�́A
![]()
![]()
�ƂȂ�܂��B
�^���ʂ͎��ʂƑ��x�̐�![]() �A�G�l���M�[�͗͂Ƌ����̐�
�A�G�l���M�[�͗͂Ƌ����̐�![]() �ł��邱�Ƃɒ��ӂ���ƁA
�ł��邱�Ƃɒ��ӂ���ƁA
![]() �܂�
�܂�
![]()
�Ƃ����A�����ꂽ�j���[�g���̉^�����������o�Ă��܂��B
�܂�A���̉F�����g�������炱���A�j���[�g���̉^�������������藧�̂��ƍl����Ǝ��R�Ȃ̂ł͂Ȃ��ł��傤���B
�j���[�g���̉^������������A�G�l���M�[�ۑ�����A�^���ʕۑ����������o���܂����A�j���[�g���̉^�������������́A�V����I�ɗ^�����܂����B
�������A���̉F�����g���ł���ƍl���邱�Ƃɂ��A�V����I�ɗ^�����Ă����j���[�g���̉^�����������A�s�m�萫�������瓱���o����̂ł��B
�܂��A���x�ɂ��Ă�
�@�A�A���
![]()
�ƂȂ�܂����A�h�u���C�̌���![]() �����
�����![]() ���g���ƁA
���g���ƁA
![]()
�ƂȂ�܂��B![]() �́A�g���̌Q���x��\���܂��̂ŁA���Ԃɑ���ʒu�̕ω����g���i�g�̂����܂�j�̑��x�ł��邱�Ƃ�s�m�萫�����͌����Ă��܂��B�܂�A��X�����q�ƃC���[�W���Ă�����̂́A���͔g�̂����܂�ł���g���Ȃ̂ł��B�����ė��q�̋O�Ղ́A���͔g���̋O�ՂȂ̂ł��B
�́A�g���̌Q���x��\���܂��̂ŁA���Ԃɑ���ʒu�̕ω����g���i�g�̂����܂�j�̑��x�ł��邱�Ƃ�s�m�萫�����͌����Ă��܂��B�܂�A��X�����q�ƃC���[�W���Ă�����̂́A���͔g�̂����܂�ł���g���Ȃ̂ł��B�����ė��q�̋O�Ղ́A���͔g���̋O�ՂȂ̂ł��B
�u���s����Ƒ��Θ_�I���q��v�ł��b�����AKlein-Gordon�����������g�̏ꍇ�A
![]()
�̕��U�W������̂ŁA�g���̌Q���x![]() �́A
�́A
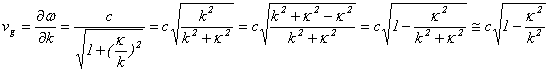
�ƂȂ�܂��i![]() �Ƃ���Ɓj�B����āA
�Ƃ���Ɓj�B����āA
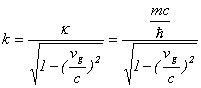
���邢�́A
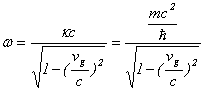
�ƂȂ�܂��B
�܂�A�g���̑��x������Ȃ������ɋ߂Â���ƁA���g���͌���Ȃ�������ɁA����Ď��Ԃ̌o�߂͌���Ȃ��O�ɋߕt���čs�����Ƃ�������܂��B
���ꂱ���AKlein-Gordon�����������Θ_�I���q��̕������ƌĂ�鏊�Ȃł��B